Find the ratio of the areas of these two regions
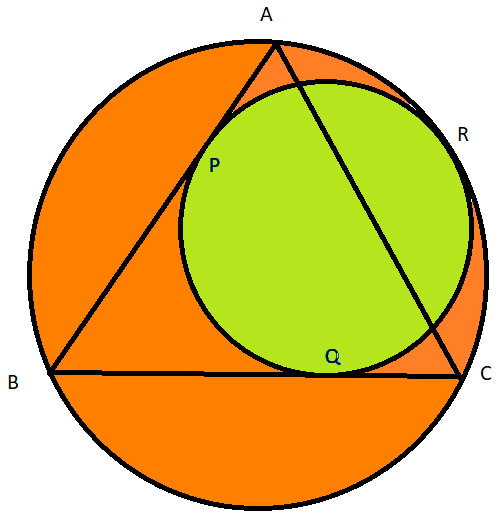
In the figure above, is an equilateral triangle inscribed in a circle. The triangle is tangent to the inner green circle at points and . The green circle is tangent to the outer circle at point .
If the ratio the areas of the orange crescent and the green circle can be expressed as , where and are coprime positive integers, find .
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since △ A B C is equilateral, the center of its circumcircle is also the centroid of △ A B C . Due to symmetry, B R is the diameter of the circumcircle. Let the radius of the circumcircle be 1 . Then diameter B R = 2 . Also let the center and radius of the green circle be O and r respectively. We note that △ B P O is a right triangle with ∠ B P O = 9 0 ∘ and ∠ P B O = 3 0 ∘ . Then we have:
B O + O R sin 3 0 ∘ r + r 2 r + r ⟹ r = B R = 2 = 2 = 3 2
Then the ratio of the areas of the orange crescent and the green circle is π r 2 π ( 1 ) 2 − π r 2 = r 2 1 − 1 = 4 9 − 1 = 4 5 . Therefore, a + b = 5 + 4 = 9 .