Find the shaded area

It can be easily seen from the figure above that the shaded region $\triangle APU$ is one of the nine equilateral triangles with side length of the hexagon. Since area of $\triangle ABC$ is 90, the area of $\triangle APU$ is $\dfrac {90}9 = \boxed{10}$ .

Relevant wiki: Length and Area Problem Solving

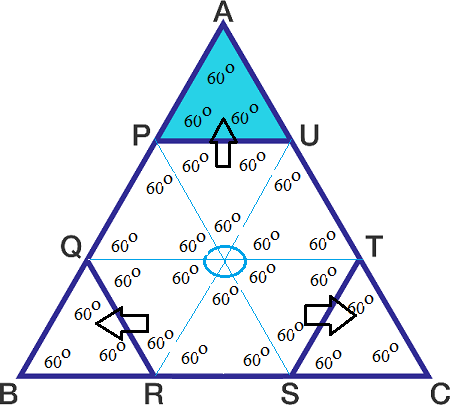
Given that it is regular hexagon. Hexagon has 6 equilateral triangle. while extend it we will get three more same equilateral triangle.

The shaded region = $\frac{1}{9}$ and the total area =90

Therefore, the Area of the shaded region = $\frac{90}{9}$ =10

Since the interior angle of regular hexgon is $120^\circ$ and on calculating the each interior triangle is $180^\circ - 120^\circ => 60°$ This shows are triangle are equilateral moreover, triangle $ABC$ is also an equilateral triangle.

Let the total length of triangle ABC be A. Then

$\frac{\sqrt3}{4} A^2 = 90$

If s be the side length of small triangle. Then $A = 3s$ Plugging $A= 3s$ in above equation

$\frac{\sqrt3}{4}(3s)^2 = 90$

$\frac{\sqrt3}{4}s^2 = \boxed{10}$

Since all the triangles are equilateral they all have the same area and so the answer becomes like this:

$\frac{\text{Total area of the triangle}}{\text{Number of triangles}}$ = area of a single triangle

So $\frac{90}{9}$ = 10

Triangles BQR, STC, and PAU are of the same area. Their total area comprises 1/3 of the area of the overall triangle, as a hexagon is equivalent to 6 small triangles here, comprising 2/3 of the area of the overall triangle. To find a small triangle's area, set up the equation as follows: 9a = 90. "a" is the area of the small triangle indicated on the illustration -- solving for it gives us 10.

It is it hard to prove that the three triangles that are cut off are equilateral. Let's say the length of the side of the given triangle is x, then the length of PU is obviously $\frac 13$ x. So the area of triangle PUA is $(\frac {1}{3})^2 \cdot 90 = 10$ .

Make 9 triangles and divide it equally

I got 10 by using the formula for area of an equilateral triangle. A=1/4(root3) times side squared. I used 3s for a side and solved for s (one side of the small equilateral triangles. Then I used s to calculate the area of one of the small triangles.

There are 9 triangles inside of hexagon

Triangle ABC is scale factor x3 of triangle APU. This means, area of ABC is 'scale factor squared' of area APU. Let area APU = y and area ABC = 90 (given). So, y x 3x3 = 90; hence y = 90/9 = 10.