Find the Shaded Region
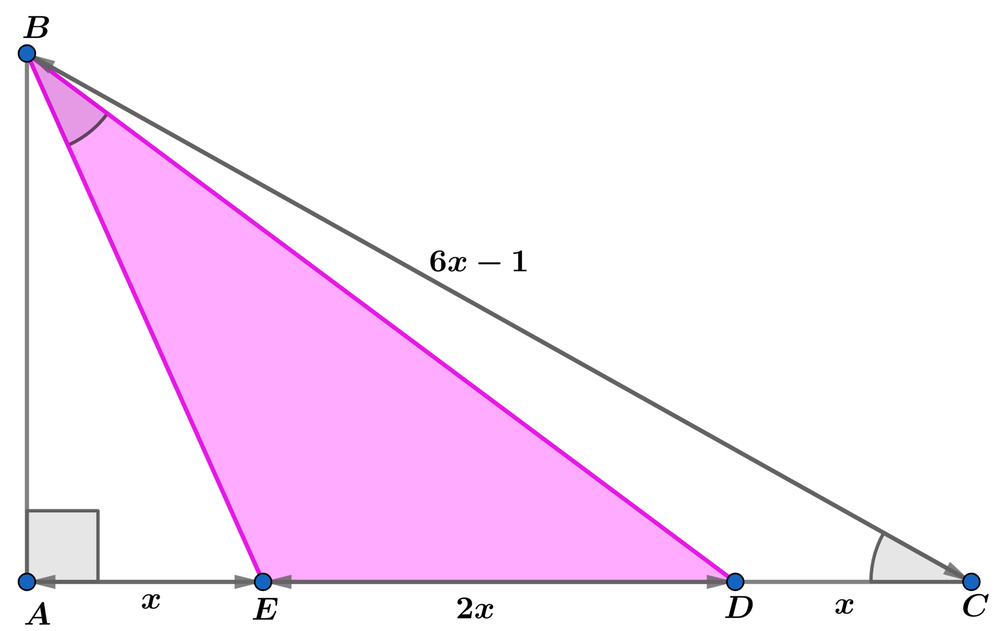
In the above diagram, ∠ B C A ≅ ∠ E B D and A E = D C = x , B C = 6 x − 1 and E D = 2 x .
If the pink area A p = β α γ α ( ω + γ γ λ ) , where α , β , γ , ω and λ are coprime positive integers, find α + β + γ + ω + λ .
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
AB² = BC² - AC²
= (6x - 1)² - (4x)²
= 20x² - 12x + 1
In the same way using Pythagoras, we get
BE² = 21x² - 12x + 1
(and
BD² = 29x² - 12x + 1
though not necessary)
Triangle BED is similar (not congruent, right?) to triangle CEB.
ED / BE = EB / CE
(ED)(CE) = BE²
6x² = 21x² - 12x + 1
15x² - 12x + 1 = 0
x = (2 ± √(7/3)) / 5
Since 6x - 1 > 0 ==> x > 1/6,
x = (2 + √(7/3)) / 5
Pink area
= x√(20x² - 12x + 1)
= √5 (19 + 2²√21) / ((3)(5²))
by substitution.
Answer
= 5 + 3 + 2 + 19 + 21
= 50
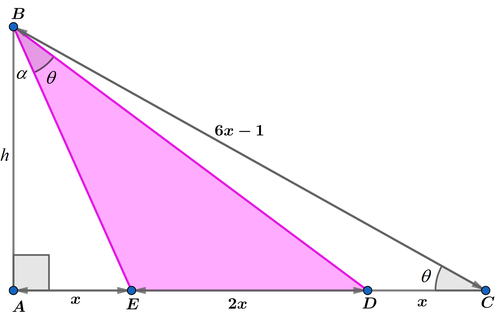
Let ∠ B C A = ∠ E B D = θ , ∠ A B E = α , and A B = h . By Pythagorean theorem ,
A B 2 h 2 = B C 2 − C A 2 = ( 6 x − 1 ) 2 + ( 4 x ) 2 = 2 0 x 2 − 1 2 x + 1
Consider tan ∠ A B D = tan ( α + θ ) ,
tan ( α + θ ) h 3 x h 3 x 9 x 2 5 x 2 1 5 x 2 − 1 2 x + 1 ⟹ x ⟹ A p = 1 − tan α tan θ tan α + tan θ = 1 − h x ⋅ 4 x h h x + 4 x h = 3 x h 4 x 2 + h 2 = 4 x 2 + h 2 = h 2 = 0 = 1 5 6 + 2 1 = 2 2 x ⋅ h = x h = 5 x 2 = 5 ( 1 5 6 + 2 1 ) 2 = 3 ⋅ 5 2 5 ( 1 9 ± 2 2 2 1 ) Note that tan α = A B A E = h x and tan θ = C A A B = 4 x h Note that h 2 = 2 0 x 2 − 1 2 x + 1 Since 6 x − 1 > 0 and h 2 = 5 x 2
Therefore the required answer is 5 + 3 + 2 + 1 9 + 2 1 = 5 0
In △ E B D we have:
λ 1 + 1 8 0 − λ 3 + λ 2 = 1 8 0 ⟹ λ 3 = λ 1 + λ 2
and tan ( λ 3 ) = x h , tan ( λ 2 ) = 3 x h and tan ( λ 1 ) = 4 x h ⟹
tan ( λ 1 ) = 4 1 tan ( λ 3 ) = 4 1 tan ( λ 1 + λ 2 )
and
tan ( λ 2 ) = 3 1 tan ( λ 1 + λ 2 ) ⟹ 4 tan ( λ 1 ) = 3 tan ( λ 2 ) ⟹
tan ( λ 2 ) = 3 4 tan ( λ 1 ) and 4 tan ( λ 1 ) = tan ( λ 1 + λ 2 ) = 3 − 4 tan 2 ( λ 1 ) 7 tan ( λ 1 ) ⟹
tan ( λ 1 ) ( 1 6 tan 2 ( λ 1 ) − 5 ) = 0 and tan ( λ 1 ) = 0 ⟹ tan ( λ 1 ) = 4 5 ⟹
h = 4 x tan ( λ 1 ) = 5 x ⟹ 2 1 x 2 = 3 6 x 2 − 1 2 x + 1 in right △ A B C
⟹ 1 5 x 2 − 1 2 x + 1 = 0 ⟹ x = 1 5 6 ± 2 1 and x = 1 5 6 − 2 1 ⟹ 6 x − 1 < 0
∴ we choose x = 1 5 6 + 2 1 ⟹ h = 5 ( 1 5 6 + 2 1 ) ⟹
A p = x h = 5 ( 1 5 6 + 2 1 ) 2 = 3 ∗ 5 2 5 ( 1 9 + 2 2 2 1 ) =
β ∗ α γ α ( ω + γ γ λ ) ⟹ α + β + γ + ω + λ = 5 0 .