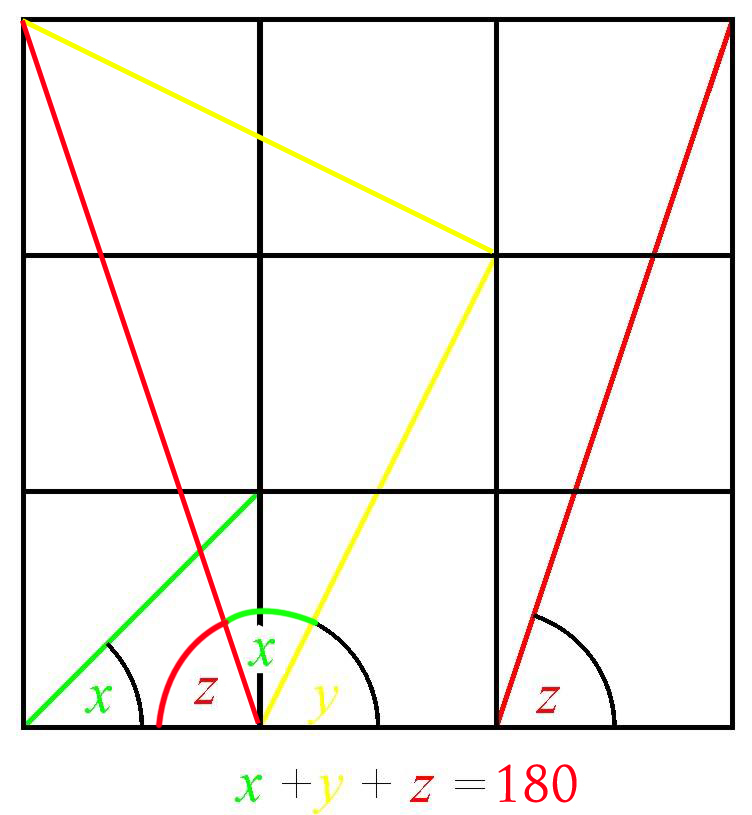
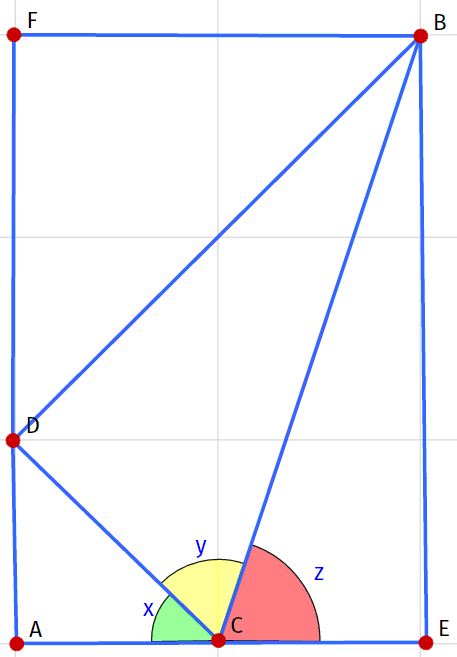
Find The Sum Of Angles
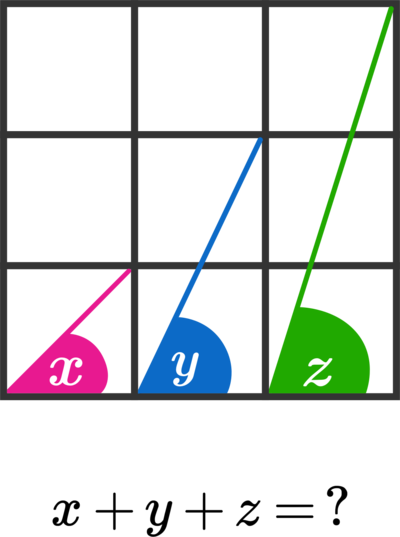
Note : The big square is divided into nine congruent squares. Give your answer in degrees.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Discussions for this problem are now closed
@Shaun Leong , doesnt line BD has a length of 2√2 not 2 (As shown by Pythagorean theorem √(1^2 + 1^2) and therefore isnt using angle y unjustified?
Basically, arctan(2√2) does not equal arctan(2)
But C D = 2 and so tan y = 2 2 2 = 2 .
A very nice solution
Beautiful.
One can also use inverse trigonometric functions
X= Arctan(1)
Y= Arctan(2)
Z = Arctan(3)
And Arctan(1) +Arctan(2) +Arctan(3) = 180
How u did this
Beautiful.
@mongol genius , how do you know that angle x is congruent to the middle of the 180° angles? I understand that the others are reflections and rotations but do not see how the last assumption is made
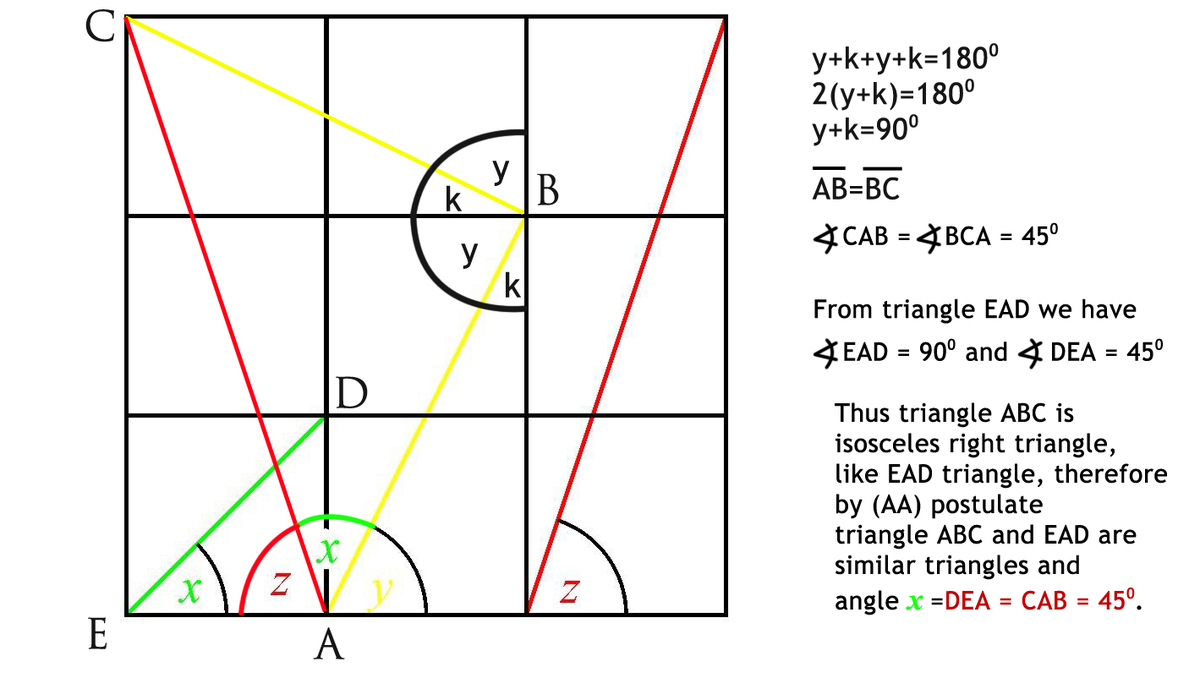
@Chase Memmer look above i have put another picture in my solution :)
Thanks! I didn't see the triangle before
tan x = 1 ⟹ x = 4 5 ∘ tan y = 2 tan z = 3
Using the sum of angles formula , we have
tan ( y + z ) = 1 − tan y tan z tan y + tan z = 1 − 2 ( 3 ) 2 + 3 = − 5 5 = − 1
Note that 0 ∘ < y < 9 0 ∘ and 0 ∘ < z < 9 0 ∘ . This gives us
0 ∘ < y + z < 1 8 0 ∘
Therefore, if tan ( y + z ) = − 1 , we know that y + z = 1 3 5 ∘
⟹ x + y + z = 4 5 ∘ + 1 3 5 ∘ = 1 8 0 ∘
Lets assume each box is made up of sides of lenght c. then tan(x) = (a / a) = 1 tan(y) = (2a / a) = 2 tan(z) = (3a /a) =3 simplifying x = tan^-1 (1) = 45 y = tan^-1 (2) = 63 z = tan^-1 (1) = 72 therefore x + y + z = 180
Mine is not a comment about how pretty the answer is, but just the calculation... t a n − 1 ( 1 ) + t a n − 1 ( 2 ) + t a n − 1 ( 3 )
Consider each line segment as a vector represented by a complex number. The green line segment is represented by 1 + i , the yellow segment by 1 + 2 i , and the red segment by 1 + 3 i . The argument of the product of these complex numbers will equal the sum of their arguments. ( 1 + i ) ∗ ( 1 + 2 i ) ∗ ( 1 + 3 i ) = ( 1 + i ) ∗ ( − 5 + 5 i ) = − 1 0 . Hence the sum of the arguments, x + y + z, equals the argument of -5 which is 180 degrees.
Actually my favourite solution so far! :)
beautiful solution
Thanks for the correction Steven. I had -5. It's now fixed.
x + y + z = tan − 1 1 + tan − 1 2 + tan − 1 3 x + y + z = 1 8 0 °
you can just plug in 1 for the length of each short segment. this way the side of the entire big square is 3. then just use sin = opp/hyp. and find the angle using arcsin on a scientific calculator. 1/root 2; 2/root 5; 3/root 10 are the ratios for the angles. find the angles for which those are the sin values and add them up. not fancy? who cares? btw, the ratios include the hypotenuse, which you would find using the Pythagorean theorem, of course
If tanA+tanB+tanC=tanAtanBtanC when A B C. Are angle of triangle.... Here it following....
Simple trigonometry: 45+tan^-1(2)+tan^-1(3)=180
It's also interesting to 'invert' the formula for tan (a+b), to get a formula for arctan x + arctan y. Then apply it here and the solution pops out.