Find the sum of the series
1 + 2 ! 1 2 + 2 2 + 3 ! 1 2 + 2 2 + 3 2 + 4 ! 1 2 + 2 2 + 3 2 + 4 2 + ⋯
If the value of the sum above can be expressed in the form of b a e , where a and b are coprime positive integers, find a + b .
Clarification:
e
≈
2
.
7
1
8
2
8
denotes the
Euler's number
.
For more problems try my set
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
WOWWWW.BEAUTIFUL SOLUTION.
This is bashing. I have forgotten a little but it might be neatly done with exponential generating function. Maybe someone can help here.
Log in to reply
Yes... Using expansion series for e x and differentiating 3 times with appropriate manipulations gives n = 1 ∑ ∞ 6 n ! n ( n + 1 ) ( 2 n + 1 ) x n − 2 1 = 3 e x ( x 2 5 + 2 9 x 2 3 + 3 x 2 1 ) Just substituting x = 1 gives the result.
Log in to reply
Yeah maybe I was mistaken. That is not really "neat". I was thinking if there was a method to find
n = 1 ∑ ∞ k = 1 ∑ n k 2 n ! 1
as a probable product of two functions. Just like we are able to find n = 1 ∑ ∞ k = 1 ∑ n k 2 x n = 1 − x 1 n = 1 ∑ ∞ n 2 x n
I will check out.
Super cool dude. I have done this by making a series of summision in e. I just love your solution.
Nice solution!!

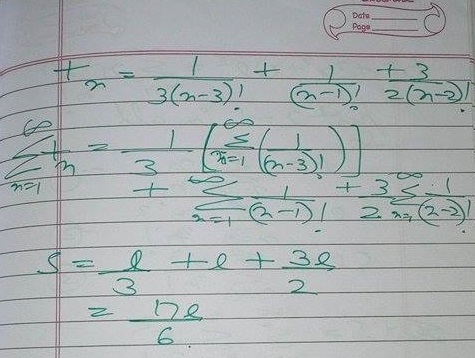
We know that:
e x = n = 0 ∑ ∞ n ! x n
Differentiating with respect to x and multiplying by x three times one gets:
x e x = n = 0 ∑ ∞ n ! n x n
( x 2 + x ) e x = n = 0 ∑ ∞ n ! n 2 x n
( x 3 + 3 x 2 + x ) e x = n = 0 ∑ ∞ n ! n 3 x n
Making x = 1 :
e = n = 0 ∑ ∞ n ! n 2 e = n = 0 ∑ ∞ n ! n 2 5 e = n = 0 ∑ ∞ n ! n 3
Then:
S = n = 1 ∑ ∞ k = 1 ∑ n n ! k 2
S = 6 1 n = 1 ∑ ∞ n ! n ( n + 1 ) ( 2 n + 1 )
S = 6 1 n = 0 ∑ ∞ n ! n ( n + 1 ) ( 2 n + 1 )
S = 6 1 ⎣ ⎡ 2 n = 0 ∑ ∞ n ! n 3 + 3 n = 0 ∑ ∞ n ! n 2 + n = 0 ∑ ∞ n ! n ⎦ ⎤
S = 6 1 [ 2 ⋅ 5 e + 3 ⋅ 2 e + e ]
S = 6 1 7 e
Thus:
a = 1 7 , b = 6 , a + b = 2 3