This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
This solution is same as Luis' s & Rakibul's solution , but with a little latex :-) ⇒
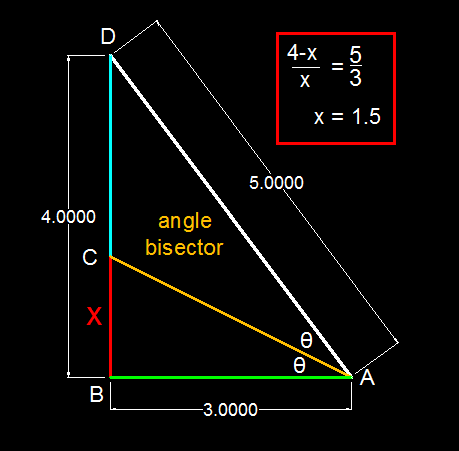
In right Δ A B D ,
tan 2 θ = 3 4 ........... ( 1 )
Similarly, in Δ A B C ,
tan θ = 3 B C .......... ( 2 )
Now , again from ( 1 ) , we have :
1 − tan 2 θ 2 tan θ = 3 4
Solving the above quadratic equation in tan θ , we get :
tan θ = − 2 , 2 1
Since tan θ > 0 ,
Therefore , tan θ = 2 1 ...... ( 3 )
Combining ( 2 ) & ( 3 ) , we get :
3 B C = 2 1
⇒ B C = 2 3
First of all, we must considerate both angles equal. So, the great angle is 2 times the angle 0. In this way, 4/3 is the tg of 2(0), and x/3 tg of (0). We considerate this, and transform tg(2(0))=4/3 in a expresion with tg(0) with the trigonometric equation of doble angle. Then of that, we make a sistem by sustitution cause tg(0)=x/3. The solution is 1.5
Here Tan@ = x/3 (x=BC); Also Tan2@= 4/3; 2tan@/(1-tan@^2)=4/3; (2X/3)/(1-x^2/9)=4/3; Solving equation we will get, X=-6 or x=3/2; Hence length cannot be negetive ao answer is 3/2=1.5;
ie. See formula for tan (2A) for the 3rd line.