Find the value of "?"

$B+G+R = \dfrac{2\,(B+G+R)}{2} =\dfrac{(G+B)+(B+R)+(R+G)}{2}=\dfrac{24+20+10}{2}=\boxed{27}$

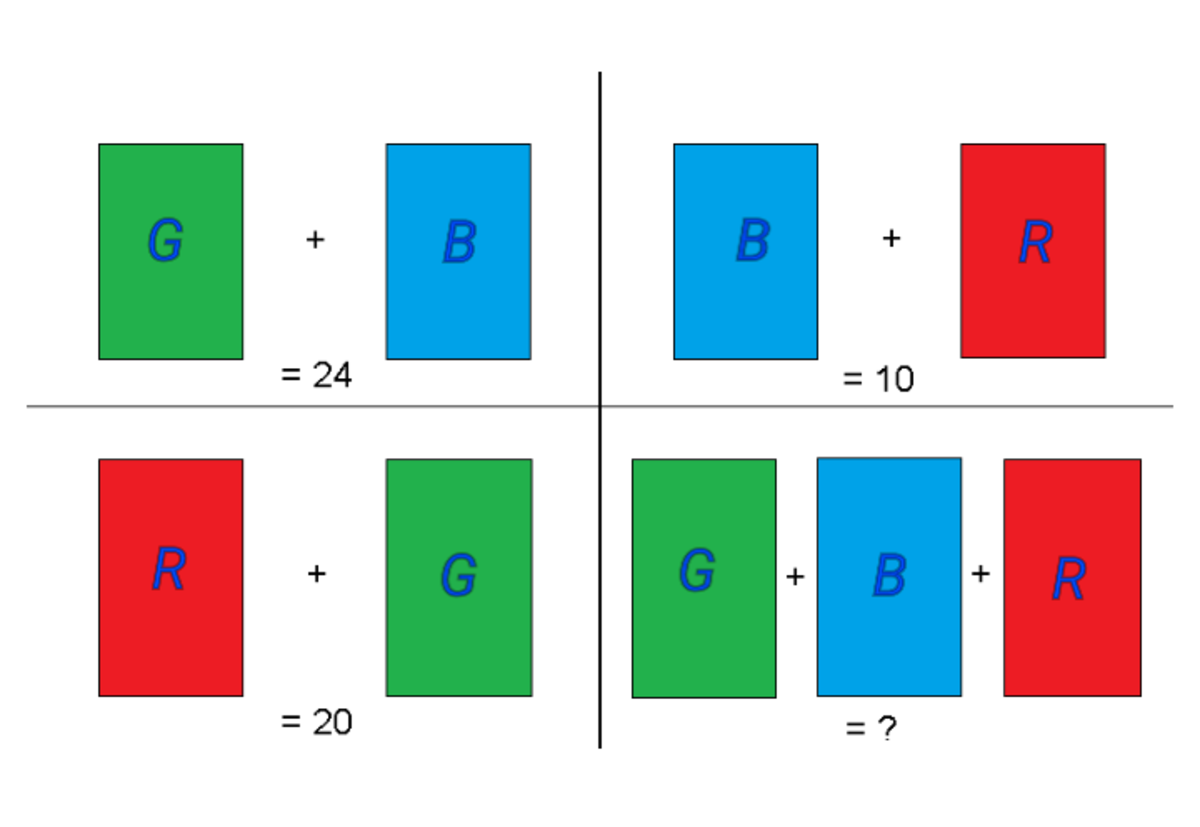
Let the green color, blue color and red color be $G,B,$ and $R$ , respectively. Then we have the three equations

$G+B=24$ $(1)$

$B+R=10$ $(2)$

$R+G=20$ $(3)$

Adding the three equations, we get

$2G+2B+2R=54$

Dividing both sides of the equation by $2$ , we get

$G+B+R=\boxed{27}$

Green+Blue=24 Blue+Red=10 Red+Green=20 2Red+2Green+2Blue=24+10+20 2 (Red+Green+Blue)=54 Red+Green+Blue=27

If you want to solve using a system or equations (the long way): Green+Blue=24 Red+Blue=10 Green-Red=14: Green=Red+14 Red+Green=20 Red+(Red+14)=20 2Red+14=20 2Red=6 Red=3 So if Red+Blue=10, Blue=7 And if Green+Blue=24, Green=17 So Green=17, Blue=7, and Red=3, meaning Red+Blue+Green=17+7+3=27

Subtract the top left box from the top right box and we get that the Green is 14 more than the red.We use the bottom right box to get the equation x+(x+14)=20.Solving,we get x(red)=3.Then we can get green is 17 and use either the top right or top left to solve that blue =7.Inputting our values(red,green,and blue),we get the answer 7+17+3=27=answer.