Find the value of this angle

My solution goes like this:

Extend the lengths of the non-bisected sides until you have a triangle instead of a quadrilateral. It already has angles of 70 and 60 degrees, so the final angle is 180 - 70 - 60 = 50 degrees.

The final vertex is also on the bisecting line which results in the bisecting line splitting the new angle in half (2 x 25 degrees), thus creating two triangles. Solving for the one in which the unknown value lies, we find that 180 - 60 - 25 = 95 degrees.

Complete the triangle. See the properties of this line (segment ) her on CTK. . So, clearly the given line is parallel to the bisector of the apex angle [ $50^{\circ}$ ] one, if we complete this triangle. The answer is $70^{\circ} + 25^{\circ} = 95^{\circ}$ $\boxed{QED}$ .

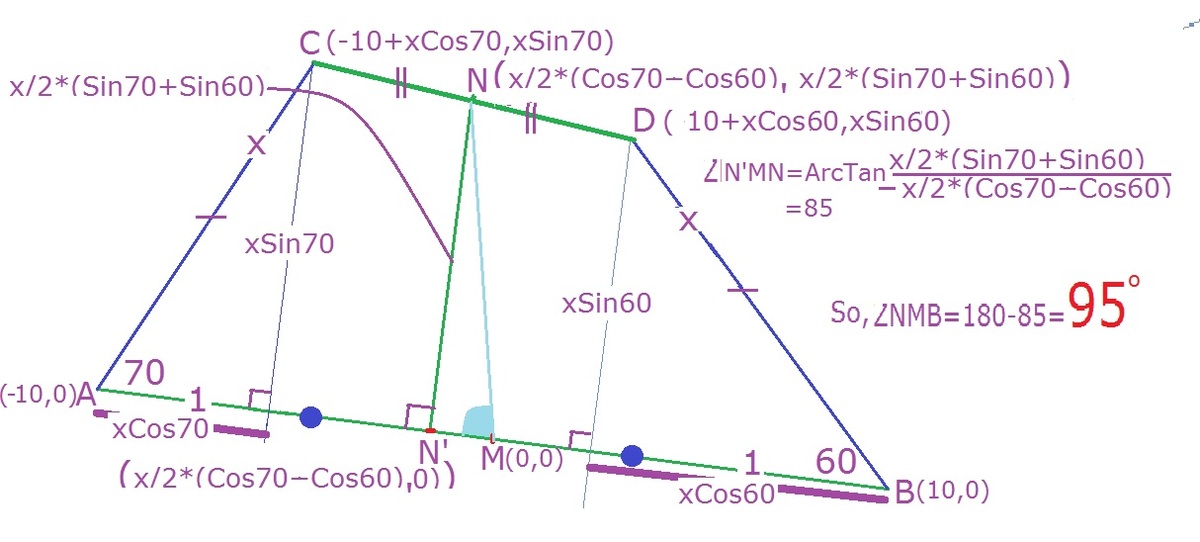WLOG Let A(-10,0), B(10,0), so AB be the bottom line, angle CAB=70 and angle ABD= 60.
M(0,0) midpoint of AB, N midpoint of CD. N' projection of N on AB.
AC=BD=x. So C(-10+xCos70, xSin70) and D(10 - xcos60, xSin60).
So N( {-10+xCos70 + 10 - xcos60 }/2, x{Sin70+Sin60}/2 ) ...so N'( x{Cos70 - cos60 }/2, 0).
ArcTanAMN= ArcTanN'MN= ArcTanNN'/N'M= ArcTan $\dfrac{x(Sin70+Sin60)/2}{-x(Cos70 - cos60 )/2}= 85^o.\\ \therefore~ BMN=180-85=\Large~~\color{#D61F06}{95^o} .$