Find the value of x in the problem #1

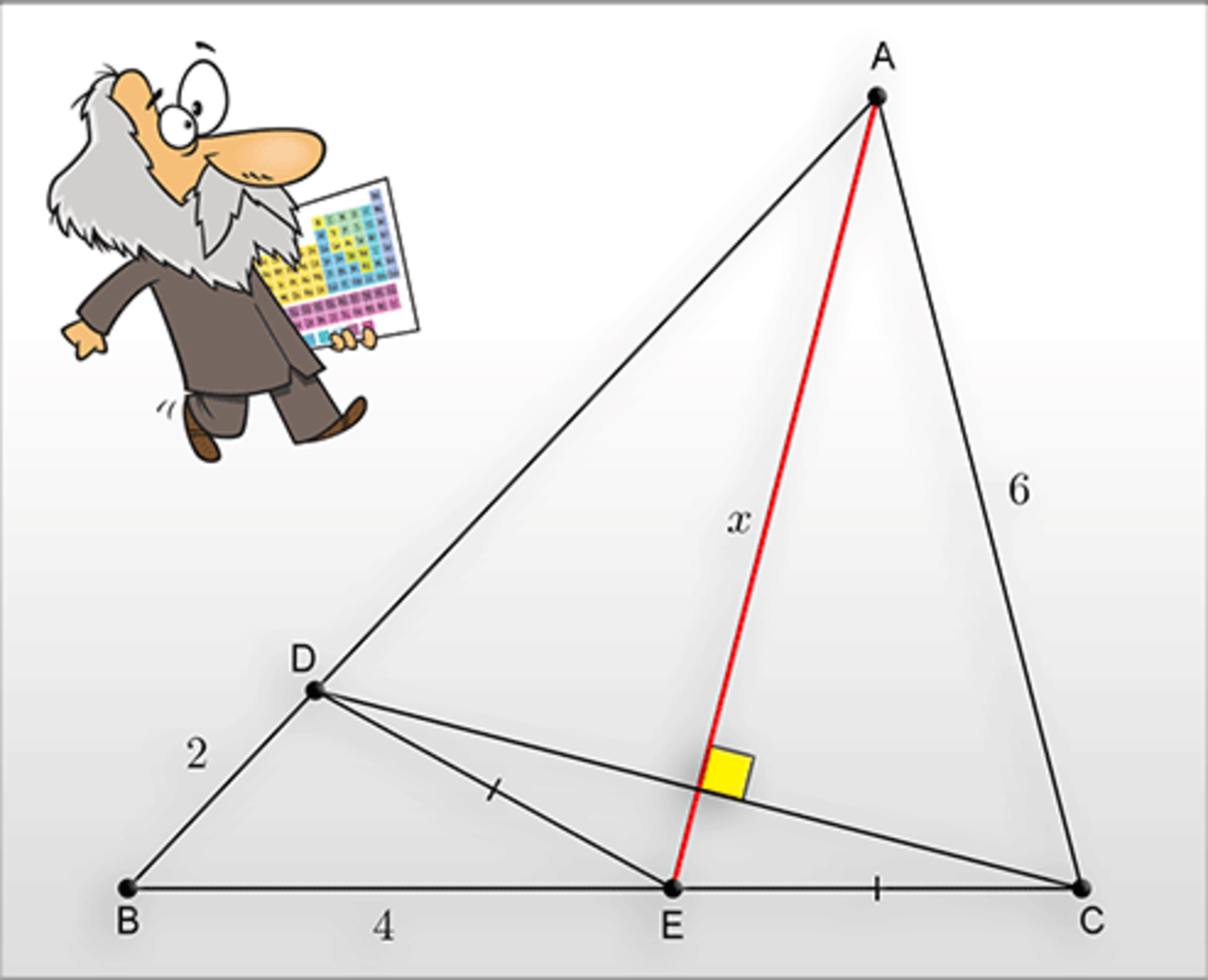
Given $DE$ = $EC$ and $AE = x$

From the figure:

$\bullet$ Consider the triangles $\Delta ODE$ and $\Delta OCE$ :

here $\ast$ $DE$ = $EC$

$\ast$ $OE$ = $OE$

$\ast$ $\angle DOE=\angle COE={ 90 }^{ \circ }$

This implies $\Delta ODE$ $\cong$ $\Delta OCE$

Therefore by congruent parts of congruent triangle $(CPCT)$ $OD$ = $OC$

$\bullet$ Similarly, we consider the triangles $\Delta AOD$ and $\Delta AOC$ :

Here $\ast$ $OD$ = $OC$

$\ast$ $OA$ = $OA$

$\ast$ $\angle AOD=\angle AOC={ 90 }^{ \circ }$

This implies $\Delta AOD$ $\cong$ $\Delta AOC$

Therefore by congruent parts of congruent triangle $(CPCT)$ $AD$ = $AC$ = $6$

$\bullet$ Now we check the similarity between two triangles $\Delta BEA$ and $\Delta BDE$ :

$\frac { AE }{ DE } = \frac { BE }{ DB } = \frac { AB }{ BE }$

we know that $AB$ = $AD+DB$ = $6+2$ = $8$ (Since we know that $AD = 6$ from second proof)

By substituting the respective values of $AB =8 , BE = 4, DB =2 , AE = x$

we get $\frac { x }{ DE } = \frac { 4 }{ 2 } = \frac { 8 }{ 4 }$

this implies $\frac { x }{ DE } = 2$ ; such that $x = 2(DE)$ ; Or $DE = EC = \frac { x}{ 2 }$

$\bullet$ Now let us take $\angle AEB = \theta$ so $\angle AEC = 180 - \theta$

In $\Delta BEA$ and $\Delta CEA$ by applying law of cosines we get

$\cos { \theta = \frac { { x }^{ 2 }+{ 4 }^{ 2 }-{ 8 }^{ 2 } }{ 8x } }$ $\longrightarrow \left( 1 \right)$ and $\cos { (180 - \theta) = \frac { { EC}^{ 2 }+{ x }^{ 2 }-{ 6 }^{ 2 } }{2\cdot EC\cdot x } }$ $\longrightarrow \left( 2 \right)$

we know that $\cos (180 - \theta$ ) = - $cos(\theta)$ and by putting $EC = \frac { x}{ 2 }$ ( From the 3 rd proof)

we reform equation $(2)$ as $-\cos { (\theta ) } =\frac { { \left( \frac { x }{ 2 } \right) }^{ 2 }+{ x }^{ 2 }-{ 6 }^{ 2 } }{ 2\cdot \left( \frac { x }{ 2 } \right) \cdot x } \longrightarrow \left( 3 \right)$

By adding equation $1$ and $3$ and on rearranging it we get a cubic equation in terms of $x$ i.e ${ x }^{ 3 }+10{ x }^{ 2 }-48x-288=0$ on solving this equation

we get $\boxed{ x = 6}$ or $\boxed{ AE = 6}$

It is clear that triat triangles ADE & ACE are congruent and, therefore, AD=AC=6 units and AE is the angle bisector of <A. Hence, AB/AC=BE/EC or BE/EC=8/6 which yields, EC=3. Now, it is a simple matter of determining the angle bisector length which is given by: x²=bc(1-(a/(b+c)²) where a=7, b=6 & c=8. Just plug in the values and obtain x²=6x8(1-(7/14)²)=48x3/4=36 or x=6 units.

$\bigtriangleup{ADE} \equiv \bigtriangleup{ACE} (\text{RHS}), \bigtriangleup{ADF} \equiv \bigtriangleup{ACF} (\text{RHA}).$

Thus, $\overline{BE} : \overline{EC}=4 : 3.$

When $\overline{DG}=a, 16-(2+a)^2=9-a^2, a=\frac{3}{4}=\overline{EF}.$

After some calculations, it is obvious that $x=\boxed{6}.$