Bounding A Triangle

Relevant wiki: Area of Triangles - Shoelace Formula

Let $P, Q$ and $R$ denote the coordinate of the intersecting points between the 3 straight lines, then

• $P$ satisfy the equations $\begin{cases} y=2x-1 \\ y = -\frac x2 + 1 \end{cases}$ .
• $Q$ satisfy the equations $\begin{cases} y=-\frac x2+1 \\ x=a \end{cases}$ .
• $R$ satisfy the equations $\begin{cases} y=2x-1 \\ x=a \end{cases}$ .

Solving these system of equations separately gives $P = \left(\dfrac45, \dfrac35\right)$ , $Q = (2-2a, a)$ and $R = \left( \dfrac {a+1}2 , a \right)$ .

Applying the shoelace formula gives

$5 = A = \dfrac12 \det \begin{vmatrix} 4/5 & 3/5 & 1 \\ 2-2a & a & 1 \\ (a+1)/2 & a & 1 \end{vmatrix} \; .$

Expanding and simplifying this equation gives $25a^2 - 40a - 84 = 0$ .

By Vieta's formula , the sum of these two values of $a$ is $- \left( \dfrac{-40}{25}\right) = \dfrac85$ . Our answer is $8+5=\boxed{13}$ .

The simplest one is to say that the other triangle would be the one congruent to the bounded triangle on the other side of origin,since length of perpendicular has to be same a-(4/5)=(4/5)+|a1| a-|a1|=(8/5) Now a-|a1| is the sum of two values of a,h hence the ans could be written as mentioned

Calculus solution: Let the two lines intersect at x=s. $2s-1= -0.5s+1 \rightarrow s=0.8$ The area of the triangle by integrals is $\displaystyle \int_s^a y_1 - y_2\mathrm{d}x = \int_s^a 2.5x-2\mathrm{d}x = [1.25x^2-2x]_s^a = 5$ $\rightarrow 1.25a^2 - 2a - 4.2 = 0 \rightarrow a = 0.8 \pm 4$ . The sum of the two possible values for a is $1.6 = \frac{16}{10} = \frac{8}{5}$ Thus $B + C = 8 + 5 =13$

First, let's find the point where the lines $y=2x-1$ and $y=-\frac{1}{2}$ intersect:

$2x-1=-\frac{1}{2}+1$

$\frac{5}{2}x=2$

$x=\frac{4}{5}$

Now we know that the lines intersect when $x=\frac{4}{5}$ . It turns out that the triangle's height towards the vertical line is $h=|a-\frac{4}{5}|$ , and the vertical side's length is $s=|2a-1-(-\frac{1}{2}a+1)|=|\frac{5}{2}a-2|$ .

The absolute values are:

When $a>\frac{4}{5}$ :

$|a-\frac{4}{5}|=a-\frac{4}{5}$ and $|\frac{5}{2}a-2|=\frac{5}{2}a-2$ .

When $a<\frac{4}{5}$ :

$|a-\frac{4}{5}|=-a+\frac{4}{5}$ and $|\frac{5}{2}a-2|=-\frac{5}{2}a+2$ .

When $a=\frac{4}{5}$ :

$|a-\frac{4}{5}|=0$ and $|\frac{5}{2}a-2|=0$ .

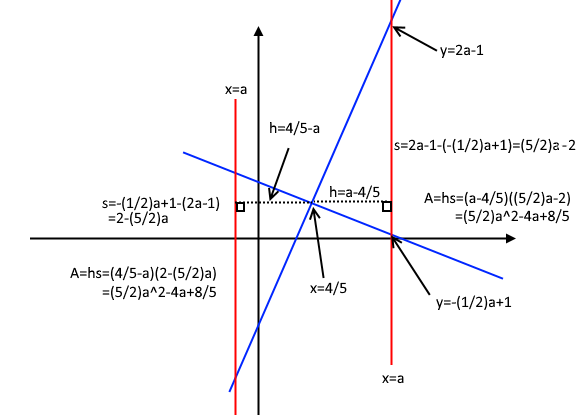
The area of the triangle is $A=\frac{hs}{2}$ .

When $a>\frac{4}{5}$ :

$A=\frac{(a-\frac{4}{5})\times(\frac{5}{2}a-2)}{2}$

When $a<\frac{4}{5}$ :

$A=\frac{(-a+\frac{4}{5})\times(-\frac{5}{2}a+2)}{2}=\frac{(a-\frac{4}{5})\times(\frac{5}{2}a-2)}{2}$

Which means that A is always

$A=\frac{(a-\frac{4}{5})\times(\frac{5}{2}a-2)}{2}=\frac{5}{4}a^2-2a+\frac{4}{5}$

We get the equation:

$\frac{5}{4}a^2-2a+\frac{4}{5}=5$

$\frac{5}{4}a^2-2a-\frac{21}{5}=0$

$25a^2-40a-84=0$

$a=\frac{40(+/-)\sqrt{40^2+4\times25\times84}}{50}$

We get:

$a_1+a_2=\frac{40+\sqrt{40^2+4\times25\times84}}{50}+\frac{40-\sqrt{40^2+4\times25\times84}}{50}=\frac{80}{50}=\frac{8}{5}$ .

Thus, $b=8$ and $c=5$ , and $b+c=8+5=\boxed{13}$ .

The sides intersect at the vertex where 2x-1=-1/2x+1, that is when x=4/5.
So the length of altitude of the triangle from this vertex=(a-4/5).
So the foot of the other altitude has x-coordinate={4/5-(a-4/5)}=(8/5-a) is the other value of a.
So sum of two value of a=a+{8/5-a}=8/5=B/C.
So B+C=8+5= $\Huge\ \ \color{#D61F06}{13}$