Find the volume of the red shaded space
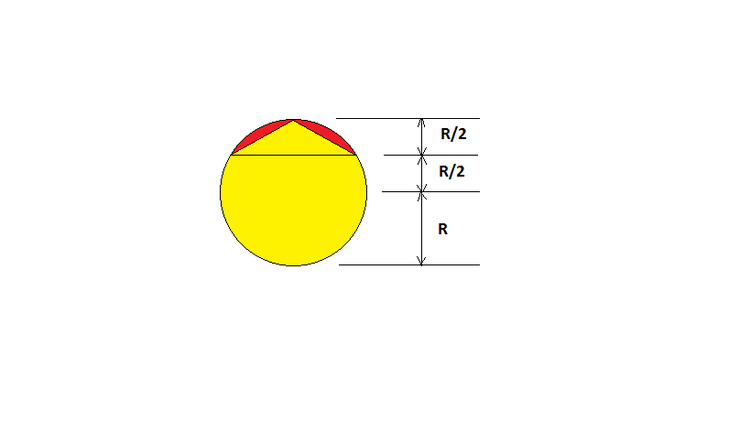A sphere is sliced at R/2 distance from the top and replaced with a right circular cone , that fits the sphere, where the height of the cone is R/2.
What is the volume of red shaded space, which is the difference between the volume of original sphere and the new object?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Divide the sphere into hemisphere, express the area of the circle as a function of height, integrate the function with respect to height from h=0 to R/2 [int(pi.(R^2 - h^2).dh , 0 , R/2)], add the volume of the other hemisphere and cone, subtract this value from the volume of whole sphere.