Find this?
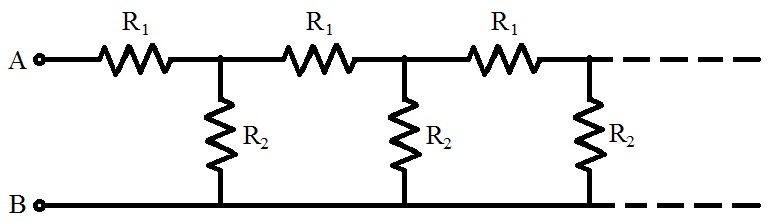
The infinite circuit shown above is formed by repetition of a same link consisting of R 1 = 4 Ω and R 2 = 3 Ω .
Find the resistance of the circuit between A and B .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Good solution,easy solution .
Log in to reply
General solution too, The same can be applied to other simple infinite circuits.
Log in to reply
@Nnsv Abhiram @Chew-Seong Cheong yes .it is applied for other infinite circuites. these method is used in other problems related to number theory....etc
I AM INSPIRED BY IRODOV
.SO THERE IS SPECIAL FORMULA FOR THIS ....
 So anwer is 6.
So anwer is 6.
@Nnsv Abhiram , you should not use all cap in text. All cap in text is equivalent to shouting in voice which is rude.
I have redone the image and wording for you.
How did you change the image?,And how did you type the ohm symbol.?
I drew the image using Print, saved it and posted it here. You can enter LaTex code by keying in \ ( [formulas] \ ) (no space between backslash \ and the brackets ()). In the LaTex backslash-brackets type \Omega Ω . \alpha α , \beta β , \gamma γ ....
@Nnsv Abhiram @Chew-Seong Cheong do anyone know the derivation of this formula?
Log in to reply
Obviously it is from the third line by solving the following quadratic equation for R .
R 2 − R 1 R − R 1 R 2 ⟹ R = 0 = 2 R 1 + R 1 2 + 4 R 1 R 2 = 2 R 1 ( 1 + 1 + 4 ( R 1 R 2 ) )
Log in to reply
@Chew-Seong Cheong Oh!! I didn't recognize it. Thanks
Let the resistance of the infinite circuit between A and B be R . Then the circuit is equivalent the circuit below where
R = R 1 + R 2 ∣ ∣ R ( R − R 1 ) ( R + R 2 ) R 2 − R 1 R − R 1 R 2 R 2 − 4 R − 1 2 ( R − 6 ) ( R + 2 ) ⟹ R = R 1 + R + R 2 R R 2 = R R 2 = 0 = 0 = 0 = 6 Ω Rearranging Putting in R 1 = 4 , R 2 = 3 Since R > 0