Find This Area
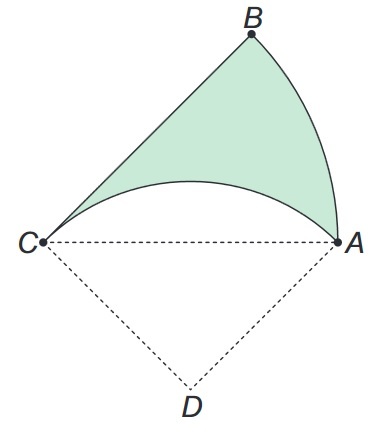
In the picture, the arc AC is one fourth of a circumference of center D and the arc AB is one eighth of a circumference of center C. The segment AD has a length of 2 cm. What is the area in cm² of the green region?
Problem from OBMEP 2017.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
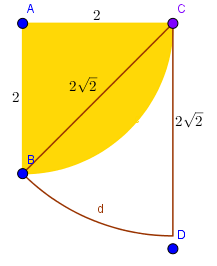
Unshaded area:
= 8 1 ( 2 2 ) 2 π − ( 4 1 ⋅ 2 2 π − 2 1 ⋅ 2 2 ) = 8 1 ⋅ 8 π − ( 4 1 ⋅ 4 π − 2 ) = π − ( π − 2 ) = π − π + 2 = 2
By Pythagorean theorem, A C = 2 2 + 2 2 = 8 = 2 2 .
It follows that B C = A C = 2 2 .
Consider sector C D A : The area of sector C D A is A = 4 1 π ( 2 2 ) = π
Consider sector A C B : The area of sector A C B is A = 3 6 0 4 5 π ( 2 2 ) 2 = 8 1 π ( 4 ) ( 2 ) = π
Area of the yellow segment is π − 2 1 ( 2 ) ( 2 ) = π − 2
Finally, the area of the green region is π − ( π − 2 ) = π − π + 2 = 2