Find this Triangle

Geometry Level 3

Consider a triangle with the following properties:

Perimeter is length 24
Distance between incenter and centroid is length 1
The line between the incenter and centroid is parallel to one of the sides

If the minimum area of this triangle is expressed as $a\sqrt b$ what is $a+b$ ?

The answer is 25.

2 solutions

David Vreken
Jan 5, 2021

Let the coordinates of the vertices of the triangle be $A(0, 0)$ , $B(p, h)$ , and $C(b, 0)$ , and let $AB = c$ , $AC = b$ , and $BC = a$ , and let the line between the incenter and centroid be parallel to side $b$ that is along the $x$ -axis. Since the perimeter is $24$ , $a + b + c = 24$ .

Since the line between the incenter and centroid is parallel to the $x$ -axis, their $y$ -coordinates will be the same, so $\cfrac{aA_y + bB_y + cC_y}{a + b + c} = \cfrac{A_y + B_y + C_y}{3}$ or $\cfrac{a \cdot 0 + bh + c \cdot 0}{24} = \cfrac{0 + h + 0}{3}$ , which solves to $b = 8$ .

Since the distance between the incenter and centroid is $1$ , $\cfrac{aA_x + bB_x + cC_x}{a + b + c} - \cfrac{A_x + B_x + C_x}{3} = \pm 1$ , or $\cfrac{a \cdot 0 + 8p + 8c}{24} - \cfrac{0 + p + 8}{3} = \pm 1$ , which solves to $c = 5$ or $c = 11$ .

If $c = 5$ then $a = 24 - b - c = 24 - 8 - 5 = 11$ , and if $c = 11$ then $a = 24 - b - c = 24 - 8 - 11 = 5$ . So either way it is a triangle with sides $5$ , $8$ , and $11$ , which by Heron's Formula has an area of $A = \sqrt{12(12 - 5)(12 - 8)(12 - 11)} = 4\sqrt{21}$ , so $a = 4$ , $b = 21$ , and $a + b = \boxed{25}$ .

While designing this problem, I noticed a an interesting pattern. If the perimeter of the triangle is $P$ and the distance between the incenter and centroid is $d$ , then the sides of the solution triangle form an arithmetic progression:

$\dfrac{P}{3}-3d, \hspace{5mm} \dfrac{P}{3}, \hspace{5mm} \dfrac{P}{3}+3d$

I haven't tried prove it, so I'll just dub it The Fletcher Conjecture. :)

Fletcher Mattox - 5 months, 1 week ago

@David Vreken : very elegant solution! And it covers the Fletcher Conjecture too:

$\frac{a\cdot 0 + bh + c\cdot 0}{P}=\frac{0+h+0}{3}$

so $b=\frac{P}{3}$

$\frac{a\cdot 0 + \frac{P}{3} p + \frac{P}{3} c}{P}-\frac{0+p+\frac{P}{3}}{3}=\pm d$

so $c=\frac{P}{3}\pm 3d$ .

This is interesting, because all the steps are reversible; if the sides of a triangle are in AP, the line joining its incentre and centroid is parallel to the side of length $\frac{P}{3}$ . (Of course, it's also a little irritating, because "the Fletcher theorem" is less catchy...)

Chris Lewis - 5 months, 1 week ago

That's a great conjecture/theorem! Thanks for sharing it.

David Vreken - 5 months, 1 week ago

If a point $X$ has a position vector that is a weighted average of the position vectors of the vertices, so that $\mathbf{x} \; = \; \alpha\mathbf{a} + \beta\mathbf{b} + \gamma\mathbf{c} \hspace{2cm} \alpha + \beta + \gamma = 1$ then the position vector $\mathbf{GX}$ (where $G$ is the centroid) is $\mathbf{x} - \mathbf{g} \; = \; (\alpha-\tfrac13)\mathbf{a} + (\beta-\tfrac13)\mathbf{b} + (\gamma - \tfrac13)\mathbf{c} \; = \; (\beta - \tfrac13)\big[\mathbf{b}-\mathbf{a}\big] + (\gamma - \tfrac13)\big[\mathbf{c}-\mathbf{a}\big]$ If $XG$ is parallel to $AB$ it follows that $\gamma=\tfrac13$ and $\alpha+\beta=\tfrac23$ , so that $\alpha,\gamma,\beta$ are in arithmetic progression.

When $X$ is the incentre, we have $\alpha = \tfrac{a}{a+b+c}$ , $\beta = \tfrac{b}{a+b+c}$ and $\gamma = \tfrac{c}{a+b+c}$ , and we deduce that $a,c,b$ are in AP.

Mark Hennings - 5 months ago

Chew-Seong Cheong
Jan 6, 2021

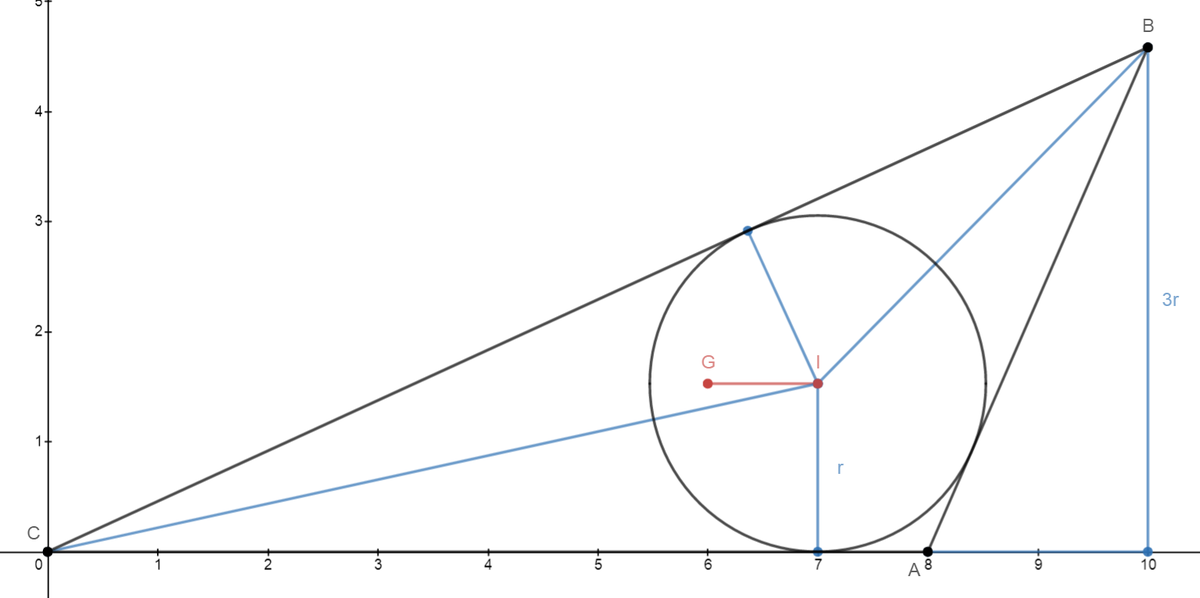
Let the triangle be $ABC$ , where $C(0,0)$ , $A(x_a,0)$ , and $B(x_b,y_b)$ with side lengths be $a$ , $b$ , and $c$ (not to be confused with the answer expression $a\sqrt b$ ). Let the incenter be $I(x_i, y_i)$ , the centroid be $G (x_g, y_g)$ and the inradius be $r$ . Then $y_i=y_g=r$ . Since $y_g = \dfrac {0+y_b+0}3$ , then $\dfrac {y_b}3 = r \implies y_b = 3r$ . This means that the height of $\triangle ABC$ is $3r$ and its area $A = \dfrac {3rb}2 = \dfrac {a+b+c}2r = 12 r \implies b = 8$ .

From Heron's formula for $s = 12$ , $b=8$ , and $c=16-a$ , we have $\sqrt{12(12-a)(8)(a-4)} = 12r \implies 3r = \sqrt{3(12-a)(a-4)}$ . We note that $x_b = \sqrt{a^2 - (3r)^2} = \sqrt{a^2 - 3(12-a)(a-4)} = 2a - 12$ .

Note that the $x$ -coordinate of $I$ is $x_i = r \cot \dfrac C2$ . From $\cos \theta = \dfrac {2a-12}a$ , we get $\cot \dfrac C2 = \sqrt{\dfrac {3a-12}{12-a}}$ and $x_i = a-4$ .

As the $x$ -coordinate of $G$ is $x_g = \dfrac {x_a+x_b+0}3 = \dfrac {2a-4}3$ and $x_i - x_g = 1$ , $\implies a-4 - \dfrac {2a-4}3 = 1 \implies a = 11 \implies r = \frac {\sqrt {21}}3 \implies A = 12r = 4\sqrt{21}$ . And the required answer is $\boxed{25}$ .

Comments: $A = 4\sqrt{21}$ is not the minimum value but the only value of area.

Find this Triangle

The answer is 25.

2 solutions

0 pending reports