Find Work Done by $\vec F$ ?

Classical Mechanics Level 3

If a force acting on a particle can be described by the equation $\vec F = \left(\dfrac{\sin y}x\right) \vec i + \left( \ln x \cos y\right) \vec j$ , then find the work done by $\vec F$ in moving an object from $\left( e, \dfrac{\pi }4 \right)$ to $\left( e^7, \dfrac{3\pi}4 \right)$ .

6\sqrt { 2 }

4\sqrt { 2 }

7\sqrt { 2 }

3\sqrt { 2 }

1 solution

Sanath Balaji
Jun 1, 2016

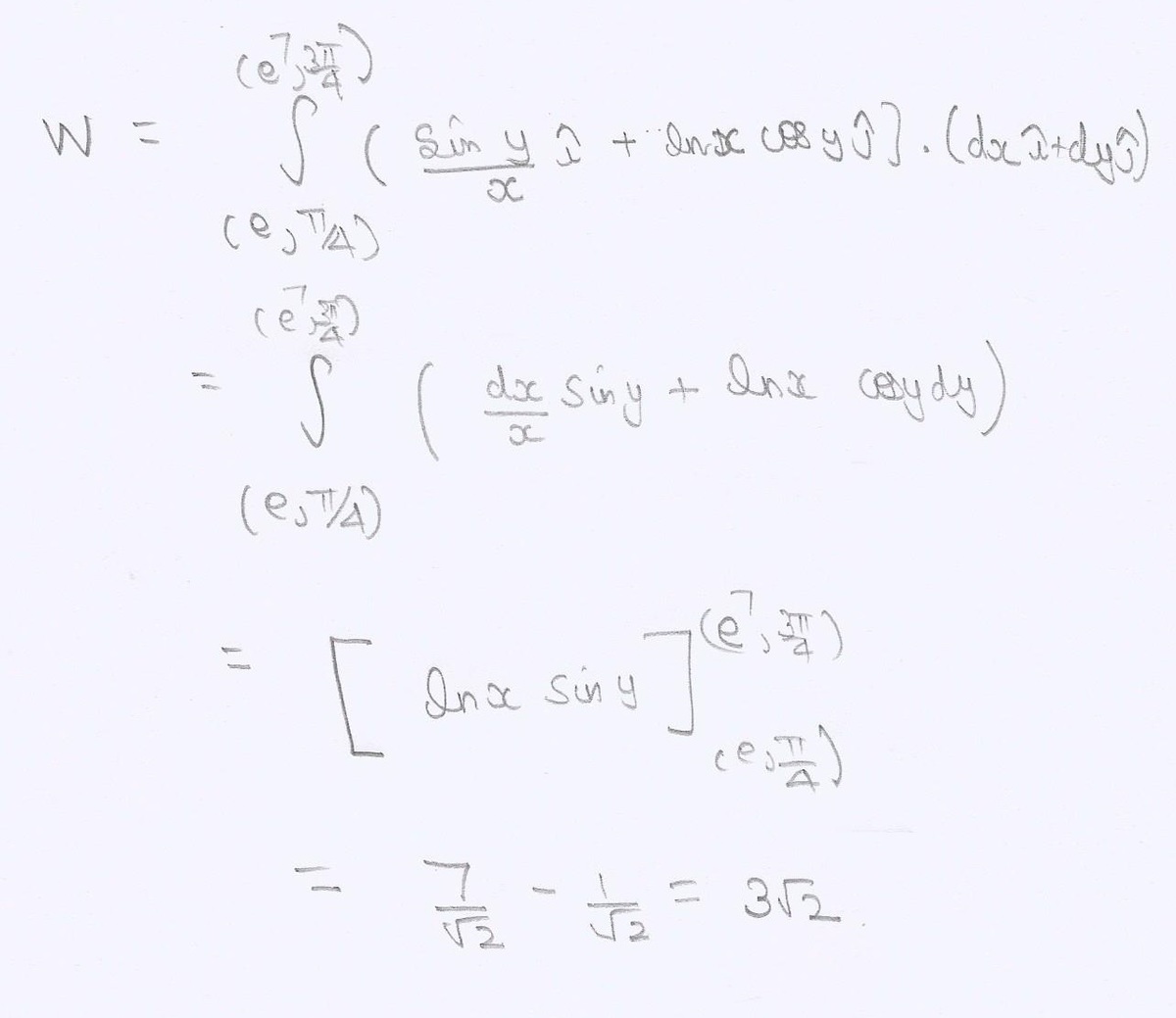
i think it should be 2 lnx siny.

AYUSH BEHERA - 5 years ago

$\quad If\quad f\left( x,y \right) =g\left( x \right) h\left( y \right) ,\\ \quad \quad \quad f^{ 1 }\left( x,y \right) =\left( g^{ 1 }\left( x \right) dx \right) h\left( y \right) +g\left( x \right) \left( h^{ 1 }\left( y \right) dy \right) \\ \quad \quad \int { \left( g^{ 1 }\left( x \right) dx \right) h\left( y \right) +g\left( x \right) \left( h^{ 1 }\left( y \right) dy \right) } =f\left( x,y \right)$

I hope it helps.

Sanath Balaji - 5 years ago

thanks i got it

AYUSH BEHERA - 5 years ago

Notice that the vector field is conservative since it is the gradient of ln(x)sin(y). So the line integral is simply the change in the value of this function between the two points (according to the gradient theorem)

Rohan Joshi - 4 months, 2 weeks ago

Find Work Done by F ⃗ \vec F F ?

1 solution

0 pending reports

Find Work Done by $\vec F$ ?