Find x

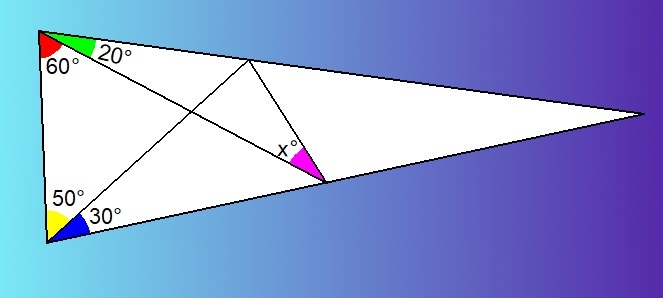
Since the angles of a triangle are preserved under uniform scaling, we can assume that the base $\text{BC} = 1$ .

It is staright-forward to see that $\triangle \text{BCD}$ is isosceles because $\angle \text{CDB} = 50^{\circ}$ .

Therefore, $\text{BC} = \text{CD} = 1$ .

Next, consider $\triangle \text{BCE}$ , applying the Law of Sines,

$\dfrac{\text{CE}}{\sin 80^{\circ}} = \dfrac{1}{\sin 40^{\circ}}$

So, $\text{CE} = \dfrac{\sin 80^{\circ}}{\sin 40^{\circ}}$

Finally, consider $\triangle \text{CDE}$ , and apply the Law of Sines again, (noting that $\angle \text{CDE} = 160^{\circ} - x$ )

$\dfrac{\text{CD}}{\sin x} =\dfrac{ \text{CE}}{ \sin (160^{\circ} - x)}$

$\text{CE} \sin x = \sin(160^{\circ} - x) = \sin 160^{\circ} \cos x - \cos 160^{\circ} \sin x$

Divide by $\cos x$ , and re-arrange,

$\tan x ( \text{CE} + \cos 160^{\circ}) = \sin 160^{\circ}$

From which, we get $\tan x = 0.57736.... = \dfrac{1}{\sqrt{3}}$ ,

Hence, $x = \tan^{-1} \dfrac{1}{\sqrt{3}} = 30^{\circ}$