Find x in square

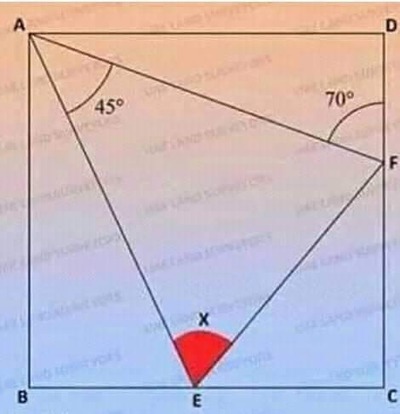
consider triangle ADF and ABE (sorry to say i still don't know how to answer which look beautiful enough in the way of math) AD=BD cos(20) AF = cos(25) AE

$\frac{AF}{AE}$ = $\frac{cos(25)}{cos(20)}$ for triangle AEF take a perpendicular to EF which go though A. now we have two triangles AOE and AOF

so AO = sin(x) AE and AO = sin(y) AF

$\frac{AF}{AE}$ = $\frac{sin (x)}{sin(y)}$ = $\frac{cos(25)}{cos(20)}$ = $\frac{sin(65)}{sin(70)}$

$\frac{x}{y}$ = $\frac{65}{70}$

x= 65k ( k is a constant) for triangle k=1

so x = 65

By angle chasing, we find that $\angle BAE = 25^\circ$ and $\angle AEB = 65^\circ$ . Then $\angle FEC = 180^\circ - 65^\circ - x^\circ = 115^\circ - x^\circ$ and

$\begin{aligned} \tan (115^\circ - x^\circ) & = \frac {FC}{CE} = \frac {1-\tan 20^\circ}{1-\tan 25^\circ} & \small \blue{\text{Let }AB=BC=CD=DA=1} \\ & = \frac {1-\tan (45^\circ - 20^\circ)}{1-\tan 25^\circ} = \frac {1-\frac {1-\tan 25^\circ}{1+\tan 25^\circ}}{1-\tan 25^\circ} \\ & = \frac {2\tan 25^\circ}{1-\tan^2 25^\circ} = \tan 50^\circ \\ 115^\circ - x^\circ & = 50^\circ \\ \implies x & = \boxed{65} \end{aligned}$