This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
nice solution sir!
take a compass put it on the screen at the angle 'x' you have your answer 40. i know it seems idiotic but try it, no use of math only a tool called compass and boom you got your answer.
"smart people never do hard works, and i do it smarty." -trupal panchal
tan x = 1 − 2 sin 2 0 ° cos 3 0 ° 2 sin 2 0 ° sin 3 0 ° = tan 4 0 ° ⟹ x = 4 0 ° .
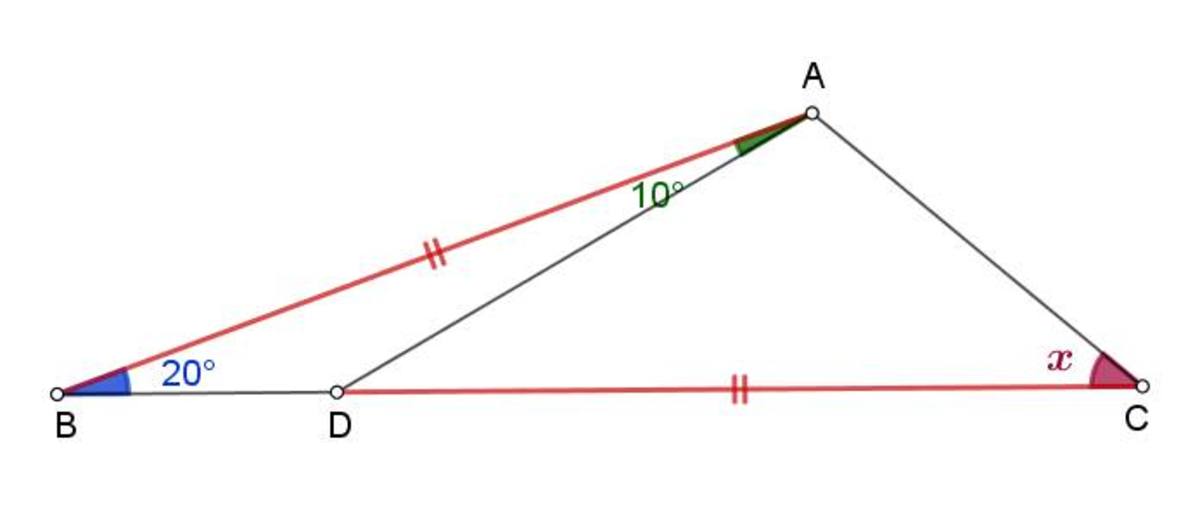
Drop a perpendicular from A to B C at E . Let A B = C D = 1 . Then ∣ A E ∣ = sin 2 0 ∘ , also
∣ D E ∣ + ∣ E C ∣ tan ∠ A D C ∣ A E ∣ + tan ∠ A C D ∣ A E ∣ tan 3 0 ∘ sin 2 0 ∘ + tan x ∘ sin 2 0 ∘ = ∣ D C ∣ = 1 = 1
⟹ tan x ∘ 1 ⟹ x = sin 2 0 ∘ 1 − tan 3 0 ∘ 1 = sin 2 0 ∘ 1 − sin 3 0 ∘ cos 3 0 ∘ = sin 2 0 ∘ sin 3 0 ∘ sin 3 0 ∘ − sin 2 0 ∘ cos 3 0 ∘ = sin 2 0 ∘ sin 3 0 ∘ sin 3 0 ∘ − cos 7 0 ∘ cos 3 0 ∘ = 2 1 ( cos 1 0 ∘ − cos 5 0 ∘ ) 2 1 − 2 1 ( cos 4 0 ∘ + cos 1 0 0 ∘ ) = sin 8 0 ∘ − sin 4 0 ∘ 1 − cos 4 0 ∘ + cos 8 0 ∘ = 2 sin 4 0 ∘ cos 4 0 ∘ − sin 4 0 ∘ 1 − cos 4 0 ∘ + 2 cos 2 4 0 ∘ − 1 = sin 4 0 ∘ ( 2 cos 4 0 ∘ − 1 ) cos 4 0 ∘ ( 2 cos 4 0 ∘ − 1 ) = 4 0