Find X of point P
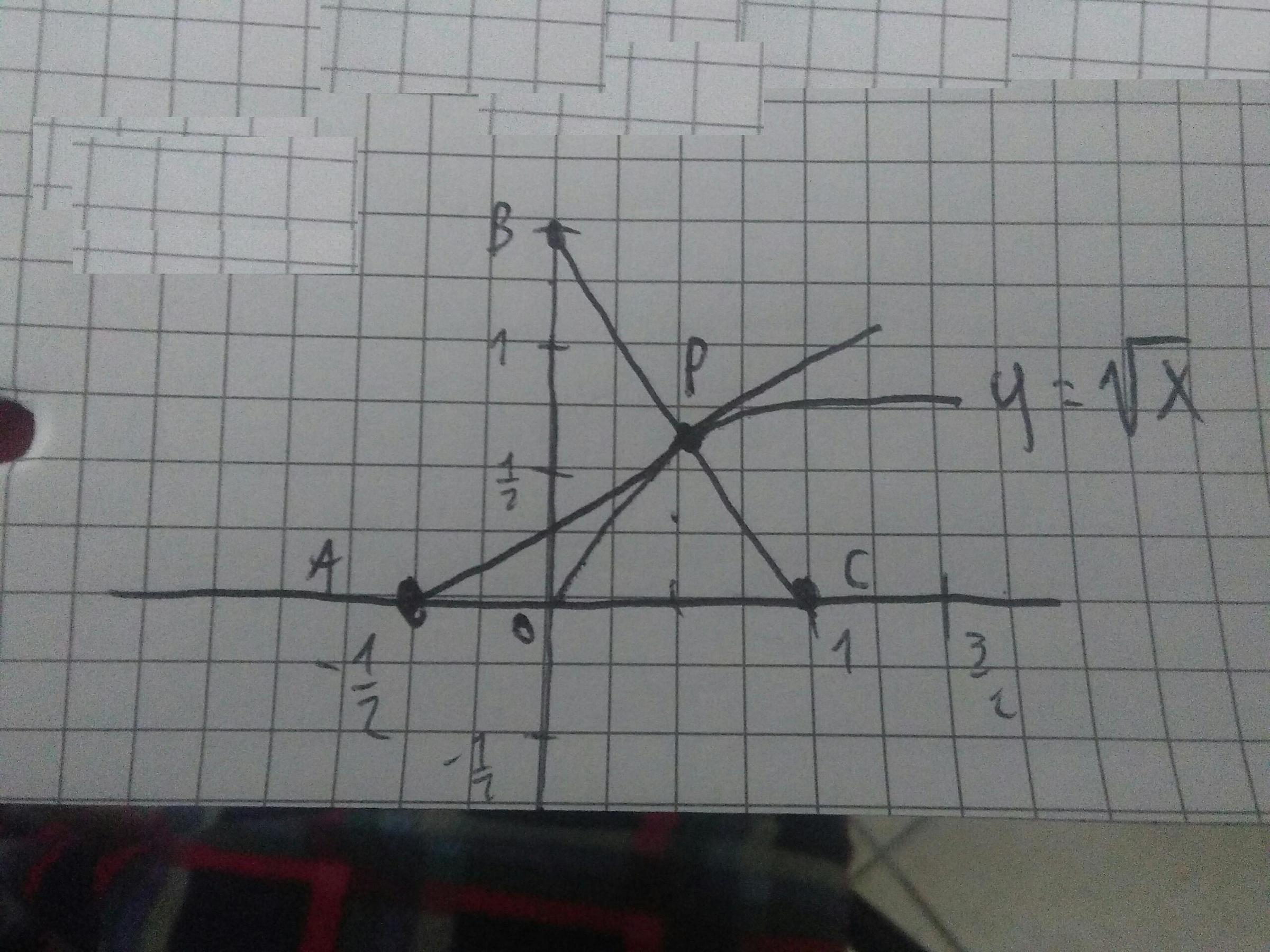
BC is perpendicular to AP; 4 times the area of triangle APC is 3 times the area of the triangle OBC
A=(-0.5;0) C=(1;0) B is on the y axis
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Frist part
Second part
Area of △ A P C = [ △ A P C ] = 2 3 ⋅ P y
Area of △ O B C = [ △ O B C ] = 1 ⋅ B y = B y
4 ⋅ [ △ A P C ] = 3 ⋅ [ △ O B C ]
4 ⋅ 2 3 ⋅ P y = 3 ⋅ B y
6 ⋅ P y = 3 ⋅ B y
B y = 2 ⋅ P y
The points P and B are on a straight line going through point C = ( 1 , 0 , therefore point P must be half way between B and C with an x -coordinate = 0 . 5 .
The problem would be more interesting if it were the y -coordinate of P that was asked for.
AP is tangent in P to the graphic of y ; if P=(Xo;Yo) I know the slope and so on ...