Finding a Angle
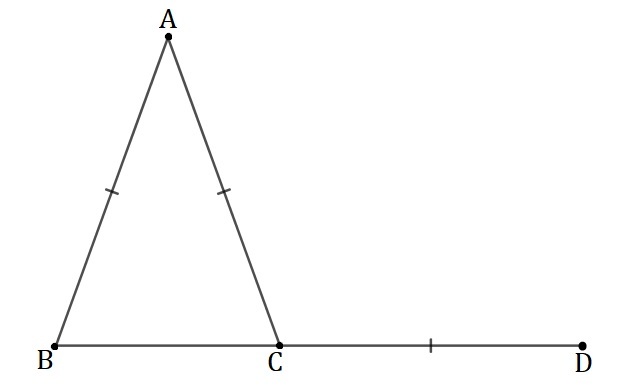
In the construction above the points B , C , and D are collinear and the point C is in between B and D . Be A the point that doesn't belongs to the segment B D such that A B = A C = C D .
If C D 1 − B D 1 = C D + B D 1 find the value of ∠ B A C in degrees.
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let x = A B = A C = C D , y = B C and θ = ∠ B A C .
Rearranging and simplifying the given equation gives y 2 + x y = x 2 . ( B D = x + y )
By the cosine rule, y 2 = 2 x 2 ( 1 − c o s ( θ ) ) , which we can reduce to y 2 = 4 x 2 s i n 2 ( θ / 2 ) . Thus, y = 2 x s i n ( θ / 2 ) .
Substituting this for y in the equation, we form the quadratic equation 4 s i n 2 ( θ / 2 ) + 2 s i n ( θ / 2 ) − 1 = 0
s i n ( θ / 2 ) = 4 − 1 + √ 5 → θ / 2 = 1 8
Therefore, θ = 3 6
Wow, this is exactly what I did 😍
C D 1 − B D 1 1 + C D B D − ( 1 + B D C D ) x + − 1 + x 1 x 2 − x + 1 x = C D + B D 1 = 1 = 0 = 0 = 2 1 + 5 = ϕ Setting x = C D B D This is the golden ratio . Thus, it has the property that ϕ = C D B C + C D = B C C D . This means that our triangle is, in fact, a golden triangle and its apex angle is 3 6 ∘ .
To see why a golden triangle has an apex angle of 3 6 ∘ , first consider an isosceles triangle with this apex angle: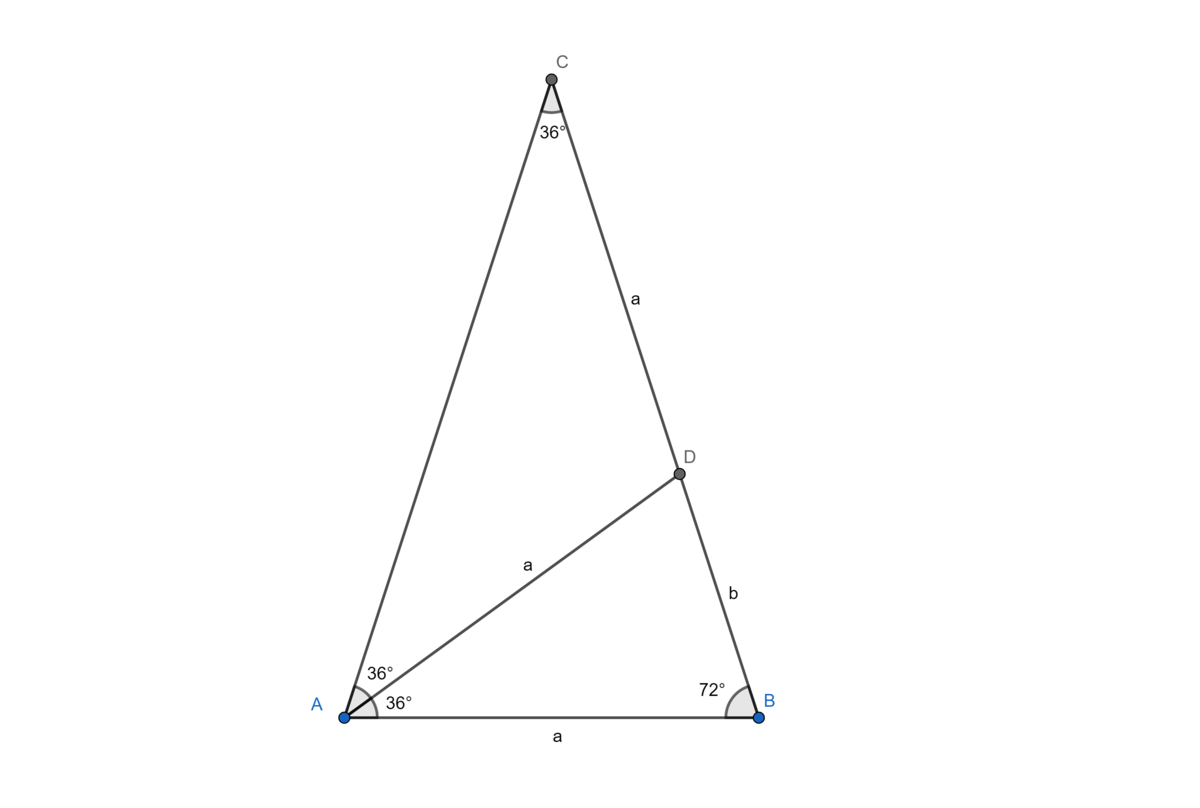 Bisect one of the base angles and label the resulting segments as shown. By similar triangles,
a
a
+
b
=
b
a
. Thus
a
a
+
b
=
ϕ
. Since the leg-base ratio of an isosceles triangle uniquely determines its angles, this is the only triangle with this property.
Bisect one of the base angles and label the resulting segments as shown. By similar triangles,
a
a
+
b
=
b
a
. Thus
a
a
+
b
=
ϕ
. Since the leg-base ratio of an isosceles triangle uniquely determines its angles, this is the only triangle with this property.