Finding area of figures
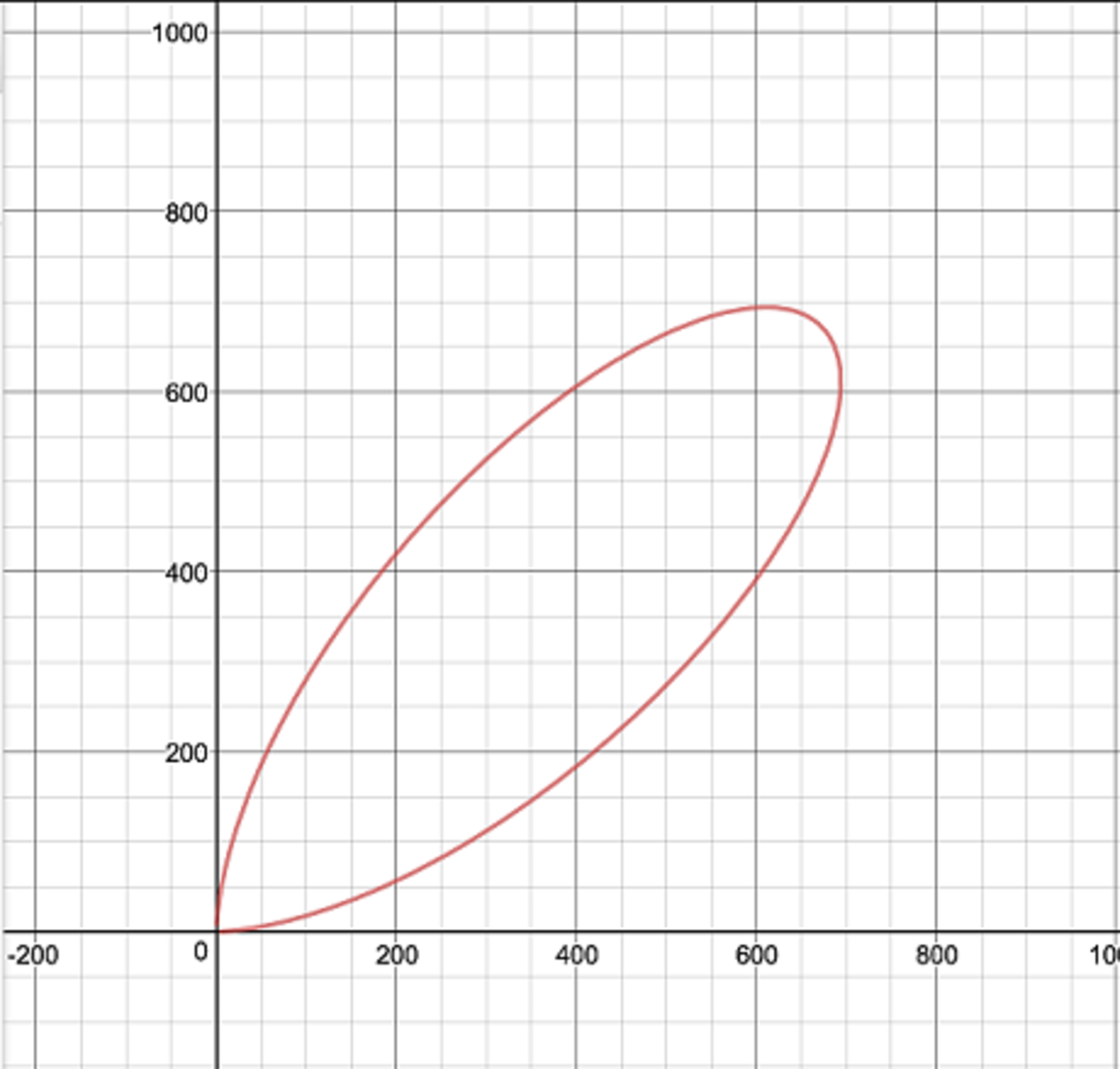
Find the area of the figure bounded by the curve:
The answer may come as: , where and are coprime.
Write your answer as .
The answer is 1353.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we will covert the cartesian equation to polar coordinates, and solve for r: r = ( cos θ ) 4 + ( sin θ ) 4 1 3 4 5 ( cos θ ) 2 3 ( sin θ ) 2 3
Second, we will use the equation to find the area of a bounded region using polar coordinates which is ∫ 2 1 r 2 d θ , our lower limit would be 0 and our upper limit would be 2 π
When we find the integral we will get 2 1 3 4 5 2 ( 4 ( 1 + ( tan θ ) 4 ) − 1 ) . Now, when plugging in the lower and upper limits we will see that it is undefined, that is we will need to take lim θ → 2 π 2 1 3 4 5 2 ( 4 ( 1 + ( tan θ ) 4 ) − 1 ) and as lim θ → 0 2 1 3 4 5 2 ( 4 ( 1 + ( tan θ ) 4 ) − 1 ) . When θ approaches 2 π the limit would be 0, and when θ aproaches 0 the limit would be 1.
Therefore, our solution would be 8 1 3 4 5 2 . Hence 1 3 4 5 + 8 = 1 3 5 3