Finding emf induced in loop
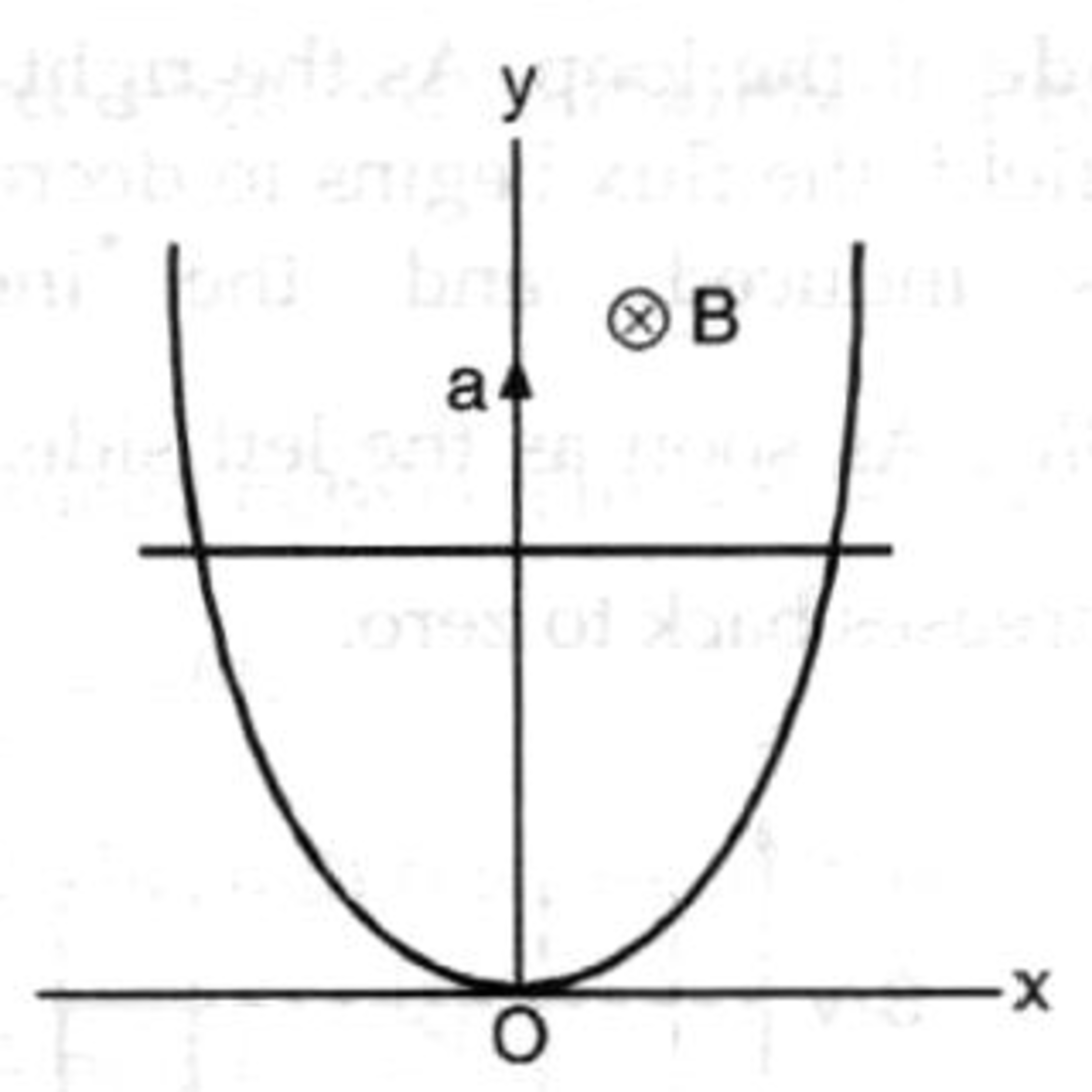
A wire bent as a parabola is located in a uniform magnetic field induction , the vector being perpendicular to the plane . At the moment a connector starts sliding translation wise from the parabola for constant apex with a constant acceleration a thus formed as a function of .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the equation of the parabola (which is not given in the problem) be y = k x 2 (I had to guess from the answer options)
Then the velocity of the connector at a position ( x , y ) , assuming it to be zero when the wire is at the apex of the parabola (this is also not given), is v = 2 k y
Area swept by the connector in time d t at that instant is d A = 2 x d y = k 2 y 2 1 d y ,
so that the rate at which the area is swept out is
d t d A = k 2 y 2 1 d t d y
= k 2 y 2 1 v
= k 2 2 a y
= k 8 a y
So the e. m. f. Induced is
E i n d = k 8 a B y
I think the ratio of E and y is asked in the problem, which is
k 8 a .