Triangles Angles: Inside and Outside
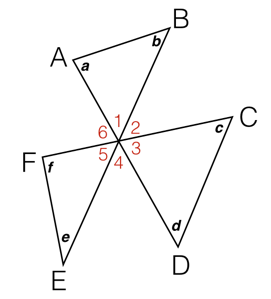
Three line segments A D , B E , C F intersect at a single point in the diagram at right.
Find the sum of the angles a + b + c + d + e + f in degrees.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Very nice experience of this question
here (a+b)=angle 2+angle 3 (ext. angle = sum of opp. int angles) similarily (c+d) = angle 4+angle 5 and (e+f)= angle 6 +angle 1
now (a+b+c+d+e+f) = angle(1+2+3+4+5+6) = 360 (angle around a point)
yes i did it in the same way
i' did it in very intrusting way, don't know whether it is right or not :) where three lines are intersecting each other it is making center so sum of angles in a circle is 360 degrees and all others angles are also derived from those so sum of all a, b, c, d, e and f angles should be 360 :) ;)
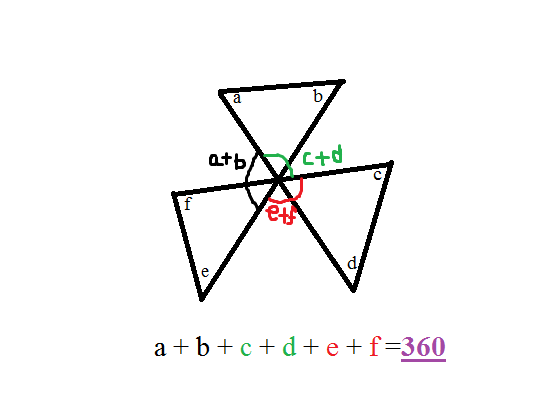 By the picture, it can easily understand why a+b+c+d+e+f = 360 .
By the picture, it can easily understand why a+b+c+d+e+f = 360 .
just move the top triangle to the bottom between the both triangle ( wich e,f and c,d). after that, the shapes is trapezium. therefore, we can find the answer. a+b+c+d+e+f = 360, because the number of trapezium (totally) is 360
How do you form a trapezium? What do you mean by "move the top triangle"? Note that if the center is point O, then triangle ABO need not be similar to triangle OED. Also, CF need not be parallel to AB.
How can you it will be a trapezium??
i imagined it was a hexagon then i imagined again that there are 6 triangles so 3/6 to 1/2 then the sum of all angles in a hexagon is 720 then i divided it into 2 then came up with 360
The points ABCDEF form an irregular hexagon and the sum of the internal angles of it is 720 ((6-2)*180). As a+b+c+d+e+f equals half of the sum of the internal angles ....
Moderator note:
It's not clear what you're doing here. Can you explain the steps?
I think he is saying that,
Join
A
F
,
B
C
,
E
D
. Now
A
B
C
D
E
F
is an irregular hexagon.
Sum of its internal angles is
7
2
0
.
So
a
+
b
+
c
+
d
+
e
+
f
will be
2
7
2
0
=
3
6
0
.
Log in to reply
Yes, that is (one of) my understanding of "ABCDEF form an irregular hexagon".
But why must a+b+c+d+e+f be half of the internal angle? Note that It is not true that a is half of ∠ B A F .
It's not clear what you're doing here. Can you explain the steps?
I let O denote the point of concurrence.
In degree measure, ∠ F O E + ∠ E O D + ∠ D O C = 1 8 0
⟹ 1 8 0 − ( e + f ) + ∠ A O B + 1 8 0 − ( c + d ) = 1 8 0
⟹ 1 8 0 − ( e + f ) + 1 8 0 − ( a + b ) + 1 8 0 − ( c + d ) = 1 8 0
⟹ 1 8 0 + 1 8 0 + 1 8 0 − 1 8 0 = a + b + c + d + e + f
⟹ a + b + c + d + e + f = 3 6 0 .
Simple. We have 6 angles. 6/3 = 2 triangles. 2 triangles, each worth 180 degrees, contain a total of 360 degrees.
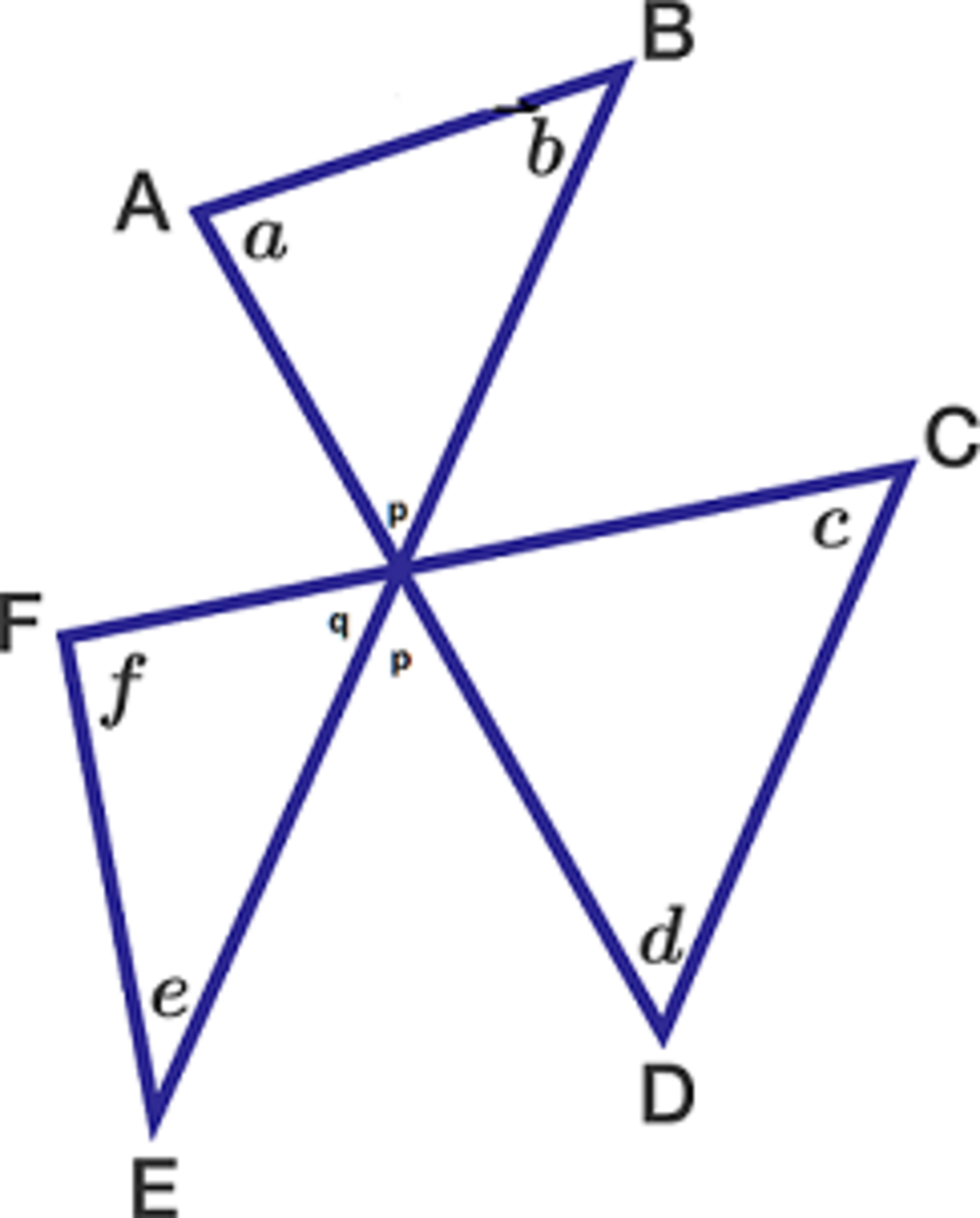
New short solution: q + p = c + d (triangle external angle & opposite angle theorems)
Therefore a + b + c + d + e + f = 360 degrees (triangles OAB, OEF each total 180 degrees. O is intersection point) ...... Q.E.D.
Each inner angle is of the form 180-A-B (or the appropriate other angles) , as well as the reflected angle. That in turn gives you 360 = 2 (180-A-B) + 2 (180-C-D) + 2*(180-E-F) Solving that gives you 360 = A + B + C + D + E + F
Using intrinsic nature of angles :
Consider putting an arrow(or a stick with something marked on one end) on A D .(Assume arrowhead is pointing A )
Rotate it to A B about point A . ∠ a is 'counted'.
Repeat the steps until all angles are 'counted'.
The arrowhead will be rotate by a 'circle' - pointing A again - counting 3 6 0 ∘
Let the centre point be O.
From the choices, the answer has to be a unique number (there is no option to select 'None of the above'). Hence the figure has to be TRUE FOR ANY 3 TRIANGLES.
Just arrange three EQUILATERAL triangles AOB, DOC, & EOF such that AD, BE & FC lie along a line.
Hence the sum is 60 x 6 = 360.
each triangle is similar to others so each angel will equal 60 so f+e=a+b = c+d so 1 equal 3 equal 5 and because 5 = 2 3 = 6 and 1 = 4 by meeting the corner so 1=2=3=4=5=6= 60° so a+b+c+d+e+f equal 360 °
Because they form triangles, ( a + b + 1 ) + ( c + d + 3 ) + ( e + f + 5 ) = 1 8 0 + 1 8 0 + 1 8 0 = 5 4 0 .
Because they form a full circle, 1 + 2 + 3 + 4 + 5 + 6 = 3 6 0 .
By Vertical Angles , 1 = 4 , 3 = 6 , and 5 = 2 .
Thus, 2 ( 1 + 3 + 5 ) = 3 6 0 , so 1 + 3 + 5 = 1 8 0 . Applying this result to the first formula, we have a + b + c + d + e + f = 5 4 0 − ( 1 + 3 + 5 ) = 5 4 0 − 1 8 0 = 3 6 0 .