Triangle In Pentagon
A composite figure consisting of a rectangle and a right isosceles triangle is shown below.
What is the area of the shaded region?
The answer is 51.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Vectors are very useful for this problem.
Let point D be the origin of the reference frame, then
D A = − 1 2 i + 5 j
D E = − 6 i − 6 j
Area = 2 1 ∣ D A × D E ∣
= 2 1 ∣ ( − 1 2 i + 5 j ) × ( − 6 i − 6 j ) ∣
= 2 1 ∣ ( 7 2 k + 3 0 k ) ∣ = 1 0 2 / 2 = 5 1
Wow. I never think about using vector to solve it. Thanks for your solution.

Let ∠ A D B = θ . We know that Δ B E D is an isosceles right triangle, right angled at E. Therefore ∠ B D E = ∠ D B E = 4 5 .
Now let D E = B E = x . Since ABDC is a rectangle A C = B D = 1 2 , A B = D C = 5 , using pythagoras in ABD A D = 1 3
In Δ D B E B E 2 + D E 2 = D B 2 x 2 + x 2 = 1 2 2 2 x 2 = 1 2 × 1 2 x 2 = 1 2 × 6 x = 6 2
Now we know that Area of a triangle is equal to 2 1 a b sin ( θ ) where θ is the angle between a and b .
∴ a r ( D B E ) = 2 1 6 2 1 3 sin ( θ + 4 5 ) sin θ = 1 3 5 , cos θ = 1 3 1 2 , sin 4 5 = cos 4 5 = 2 1 ⟹ a r ( D B E ) = 3 2 × 1 3 × ( sin θ cos 4 5 + cos θ sin 4 5 ) = 3 2 × 1 3 × ( 1 3 5 2 1 + 1 3 1 2 2 1 ) = 3 × ( 5 + 1 2 ) = 3 × 1 7 ∴ a r ( D B E ) = 5 1
Since the triangle BDE is isosceles, the angels EBD and BDE are both equal to 45 degree. By drawing an axis of symmetry of the figure, we can easily obtain two isosceles triangles, BNE and DNE. So, NE = BN = DN = 6. It can be easily check that MN = 2.5.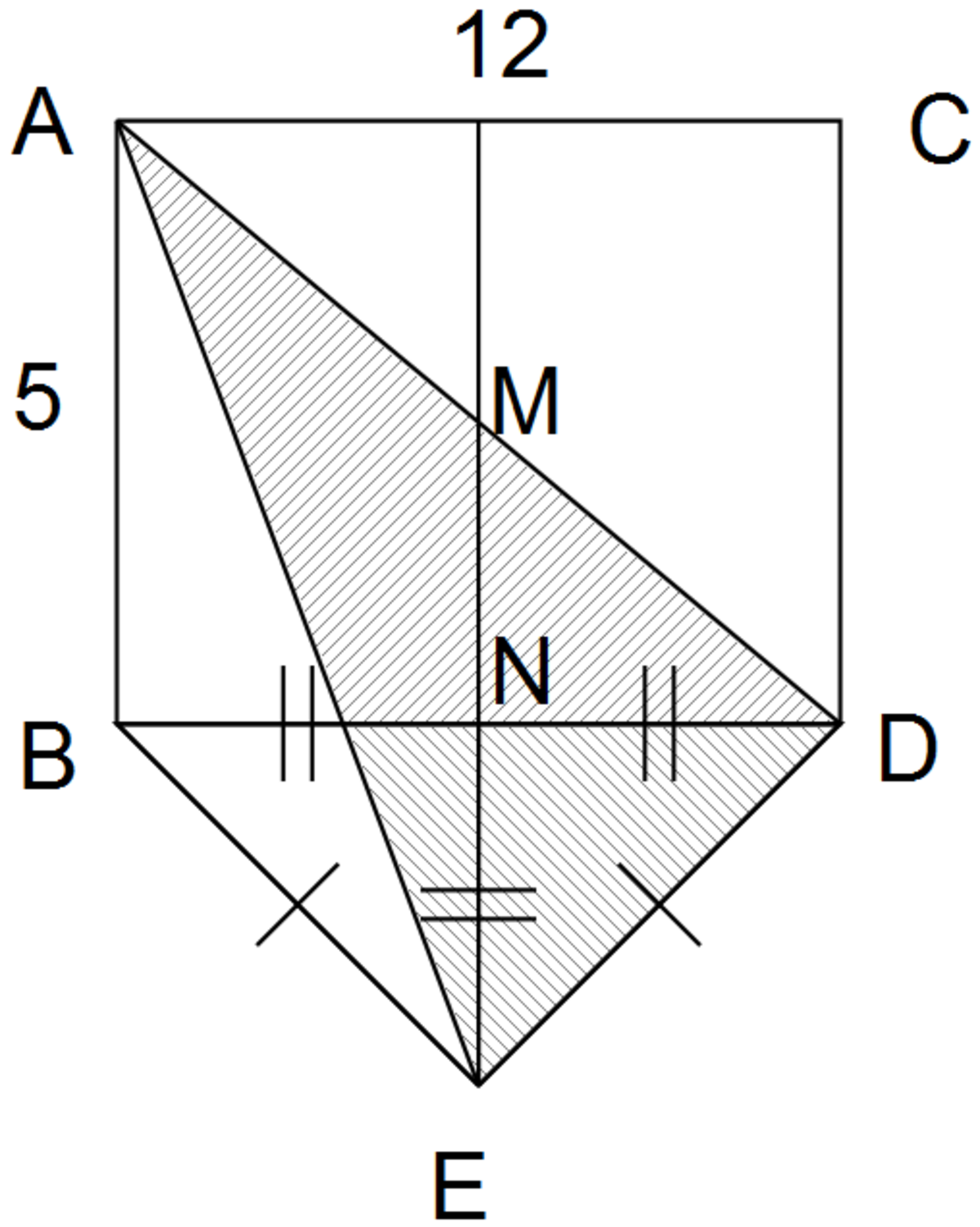
The shaded region can be divided into two triangles, AME and DME. Both of them have height 6 and base length 8.5. Thus the shaded region has area 2 x 1/2 x 8.5 x 6 = 51.