Finding the mass

Algebra Level pending

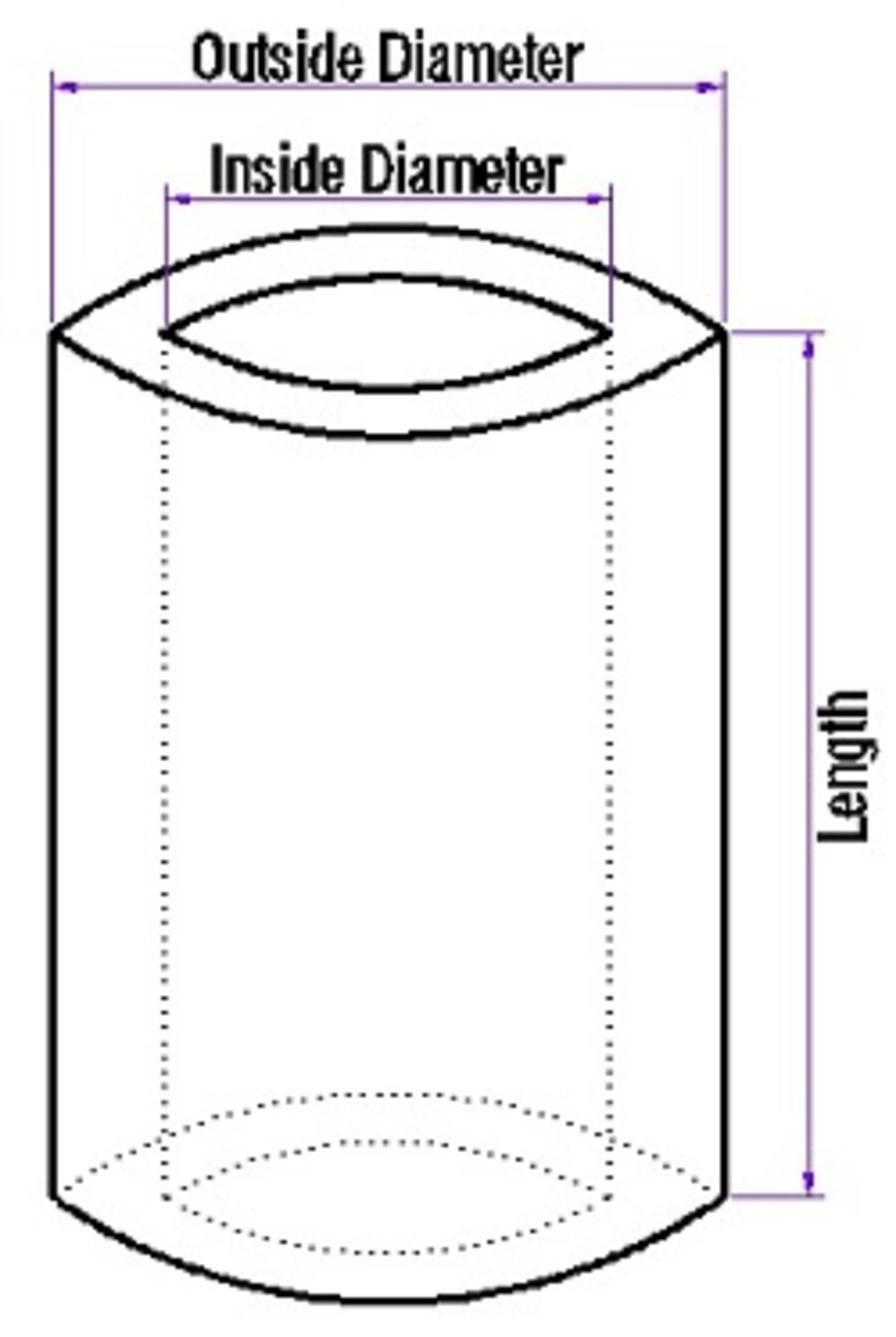A pipe is in the form of a hollow cylinder as shown in the figure above. Find its mass in kilograms when its length is $1.5$ $m$ , its outside diameter is $300$ $mm$ , its inside diameter is $200$ $mm$ and its density is $5500$ $\frac{kg}{m^3}$ .

Round off your answer to the nearest whole number.

The answer is 324.

1 solution

A Former Brilliant Member
Mar 27, 2017

Use the formula: $m = ρv$ where: $m=mass$ , $ρ=density$ and $v=volume$

Solving for the volume

let $v$ =volume of the pipe, $v_1$ = volume of the bigger cylinder and $v_2$ = volume of the smaller cylinder

$v =$ $v_1 - v_2 = \frac{π}{4}(0.3^2)(1.5) - \frac{π}{4}(0.2^2)(1.5) = 0.058904862$ $m^3$

Solving for the mass

$m = ρv = (5500)(0.058904862) = 324$ $kg$

Finding the mass

The answer is 324.

1 solution

0 pending reports