Finding Middle Ground
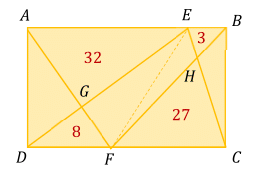
A rectangle is divided by four lines, as shown, with 4 of the resulting triangles having known areas. Find the area of the quadrilateral that is shaded in pink.
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Best method
 △
A
E
G
and
△
F
D
G
are similar with areas in ratio of
3
2
:
8
=
4
:
1
. Their respective lengths are therefore in the ratio
4
:
1
=
2
:
1
. So if the height of the
△
F
D
G
perpendicular to
F
D
is
h
, then the height of
△
A
E
G
perpendicular to
A
E
is
2
h
and the height of
△
A
E
F
perpendicular to
A
E
is
3
h
.
△
A
E
G
and
△
F
D
G
are similar with areas in ratio of
3
2
:
8
=
4
:
1
. Their respective lengths are therefore in the ratio
4
:
1
=
2
:
1
. So if the height of the
△
F
D
G
perpendicular to
F
D
is
h
, then the height of
△
A
E
G
perpendicular to
A
E
is
2
h
and the height of
△
A
E
F
perpendicular to
A
E
is
3
h
.
Since △ A E F and △ A E G have the same base A E and height of A E F is 2 3 of the height of △ A E G the area A A E F = 2 3 × A A E G = 2 3 × 3 2 = 4 8 .
A E G F = A A E F − A A E G = 4 8 − 3 2 = 1 6
The ratio of A F H C : A B H E = 2 7 : 3 = 9 : 1 so in the similar triangles F H C and B H E the ratio of sizes is 3 : 1 .
h F H C = 3 × h B H E , h F E C = 4 × h B H E
Therefore A F E C = 3 4 × A F H C = 3 4 × 2 7 = 3 6
A F H E = A F E C − A F H C = 3 6 − 2 7 = 9
A G E H F = A E G F + A F H E = 1 6 + 9 = 2 5
Such a delightfully clever solution! Could we leverage the fact that triangles AEG and ABF have bases and heights in ratios 4:5 and 2:3? Then the area of triangle ABF = 32 (5/4)(3/2) = 60
It can be simplified as such: Triangle ABF occupies half the area of the full rectangle. Notice that Area of triangle DFG + Area of triangle HFC = Area of triangle AEG + Area of triangle EBH. Hence the region in pink is simply the sum of areas of triangles AGD and BHC. Note that triangle AEG is similar to triangle FDG. Hence the ratio of FG to AG is 1:2. Area of triangle AGD is thus 8 x 2 = 16. Note that triangle EBH is similar to triangle CFH. Hence the ratio of FH:CH is 1:3. Thus, Area of triangle BHC = 3 x 3 = 9. 16 + 9 = 25 is our desired solution.
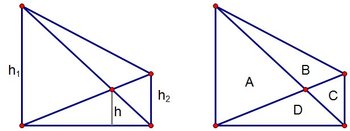
The Crossed Ladders Theorem tells us that h 1 = h 1 1 + h 2 1 = h 1 h 2 h 1 + h 2 and hence we have the following identities concerning the areas: D 1 = A + D 1 + C + D 1 = ( A + D ) ( C + D ) A + B + C + D These equations can be rearranged to read B = D = A C Thus the area of the shaded region is 8 × 3 2 + 3 × 2 7 = 1 6 + 9 = 2 5 .
Moderator note:
This is related to the harmonic mean ; h is half the harmonic mean of h 1 and h 2 .
Slight typo: 1/(A+D) should read 1/(A+B)
Log in to reply
Since A + B = A + D , this is not a typo, but a matter of choice!
interesting. ithink . wait i need to go poop
why did you write (A+B+C+D)/((A+D)(C+D)) instead of (A+C+2D)/((A+D)(C+D)) ??
Log in to reply
The second set of equations, involving A , B , C , D is the translation of the first set, involving h , h 1 , h 2 . The fact that A + C + 2 D = A + B + C + D is one of the facts needed to solve the problem. It tells us that B = D , for example.
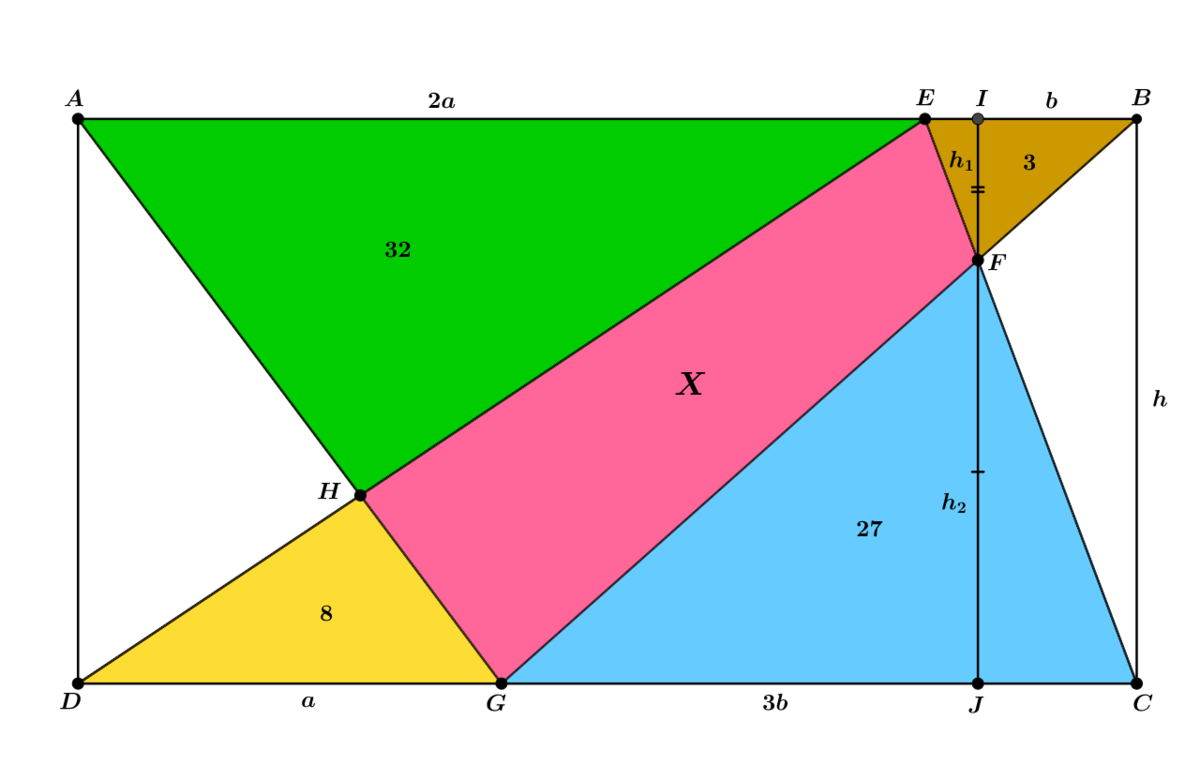
Let the area of the required region be X
From the above figure we can see that ,
Δ A E H and Δ G D H are similar
A E D G Let, DG ⟹ A E = Area of Δ A E H Area of Δ G D H = 3 2 8 = 2 1 = a = 2 a
Similarly, Δ E B F and Δ C G F are similar
G C E B Let, EB ⟹ G C = Area of Δ C G F Area of Δ E B F = 2 7 3 = 3 1 = b = 3 b
A B C D is a rectangle
⟹ A B ⟹ 2 a + b ⟹ a ⟹ A B = D C = a + 3 b A B = A E + E B , D C = D G + G C = 2 b = 2 ( 2 b ) + b = 5 b ( 1 )
Let B C = h
from the figure it is easy to see that h = h 1 + h 2
Area of Δ E B F h 1 Similarly, h 2 h = 2 1 ⋅ b ⋅ h 1 = b 2 ⋅ ( Area of Δ E B F ) = b 6 = 3 b 2 ⋅ ( Area of Δ C G F ) = 3 b 5 4 = b 1 8 = h 1 + h 2 = b 2 4 ( 2 )
We have ,
Area of rectangle A B C D = A B ⋅ B C = 5 b ⋅ b 2 4 From ( 1 ) and ( 2 ) = 1 2 0
Now, we have ,
Area of Δ D E C = Area of Δ A G B ⟹ Area of Δ D E C + Area of Δ A G B ( 8 + 2 7 + X ) + ( 3 2 + 3 + X ) 7 0 + 2 X X = 2 1 ⋅ ( Area of rectangle A B C D ) = Area of rectangle A B C D = 1 2 0 = 1 2 0 = 2 5
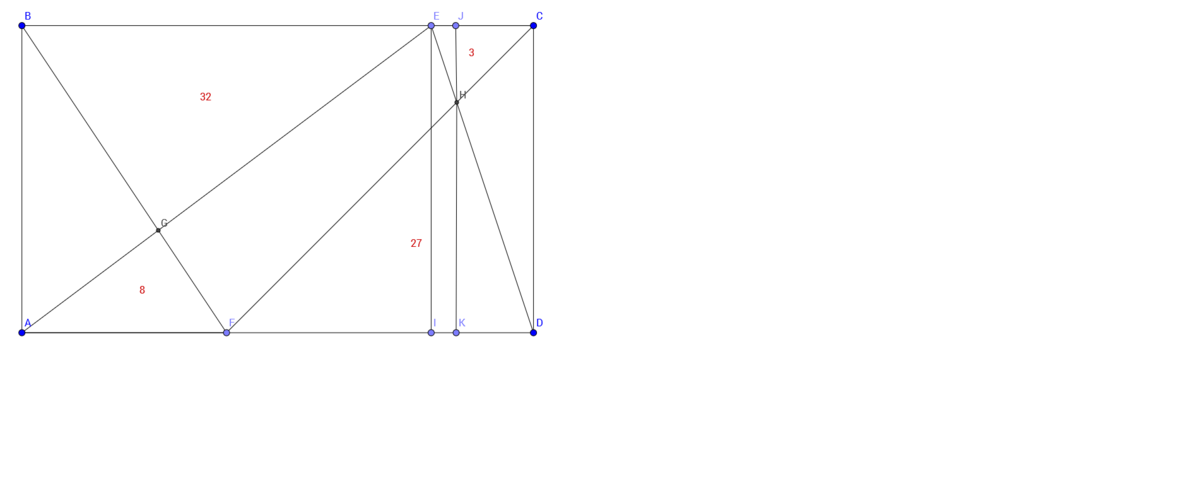 We have 2 pairs of similar triangles -
△
A
G
F
and
△
B
E
G
with area ratio
1
:
4
, and
△
E
C
H
and
△
F
H
D
with area ratio
1
:
9
. The corresponding length ratios are thus
1
:
2
and
1
:
3
.
We have 2 pairs of similar triangles -
△
A
G
F
and
△
B
E
G
with area ratio
1
:
4
, and
△
E
C
H
and
△
F
H
D
with area ratio
1
:
9
. The corresponding length ratios are thus
1
:
2
and
1
:
3
.
∣ B E ∣ = 2 ∣ A F ∣ , ∣ F D ∣ = 3 ∣ E C ∣
∣ B E ∣ + ∣ E C ∣ = ∣ A F ∣ + ∣ F D ∣ ⟹ 2 ∣ A F ∣ + ∣ E C ∣ = ∣ A F ∣ + 3 ∣ E C ∣ ⟹ ∣ A F ∣ = 2 ∣ E C ∣
∣ B C ∣ = ∣ A D ∣ = 5 ∣ E C ∣
∣ H K ∣ = 3 ∣ J H ∣ ⟹ ∣ E I ∣ = ∣ J K ∣ = ∣ J H ∣ + 3 ∣ J H ∣ = 4 ∣ J H ∣
A E C H A A E D = 2 1 ∣ E C ∣ ∣ J H ∣ 2 1 ∣ A D ∣ ∣ E I ∣ = ∣ E C ∣ ∣ A D ∣ × ∣ J H ∣ ∣ E I ∣ = 5 × 4 = 2 0 ⟹ A A E D = A E C H × 2 0 = 3 × 2 0 = 6 0
A G E H F = 6 0 − 8 − 2 7 = 2 5
And here is another solution:
First, as above, we recognize the similar triangles. The top side of the rectangle is divided as 2 a + b ; the bottom side as a + 3 b . Equating these, 2 a + b = a + 3 b ∴ a = 2 b , and we see that the divisions are really 4:1 at the top and 2:3 at the bottom.
Now consider the truncated triangle formed by the green, blue, and pink sections. Its height is the height of the rectangle; its average width is the mean of 4 / 5 and 3 / 5 of the width of the rectangle; its area is therefore 7 / 1 0 th of the area U of the rectangle. We write 5 9 + A = 1 0 7 U . Likewise, consider the combination of yellow, pink, and brown. Its average width is the mean of 1 / 5 and 2 / 5 of the width of the rectangle. Thus we have 1 1 + A = 1 0 3 U .
Compare the two areas as a ratio: 1 1 + A 5 9 + A = 3 7 ∴ 1 7 7 + 3 A = 7 7 + 7 A ∴ 1 0 0 = 4 A ∴ A = 2 5 .