Finding the number of shortest paths
Probability
Level
3
An ant is at point A. It wants to go to point B in shortest possible path staying on the grid lines (i.e. it can only go right and up). In how many ways it can go to B from A?
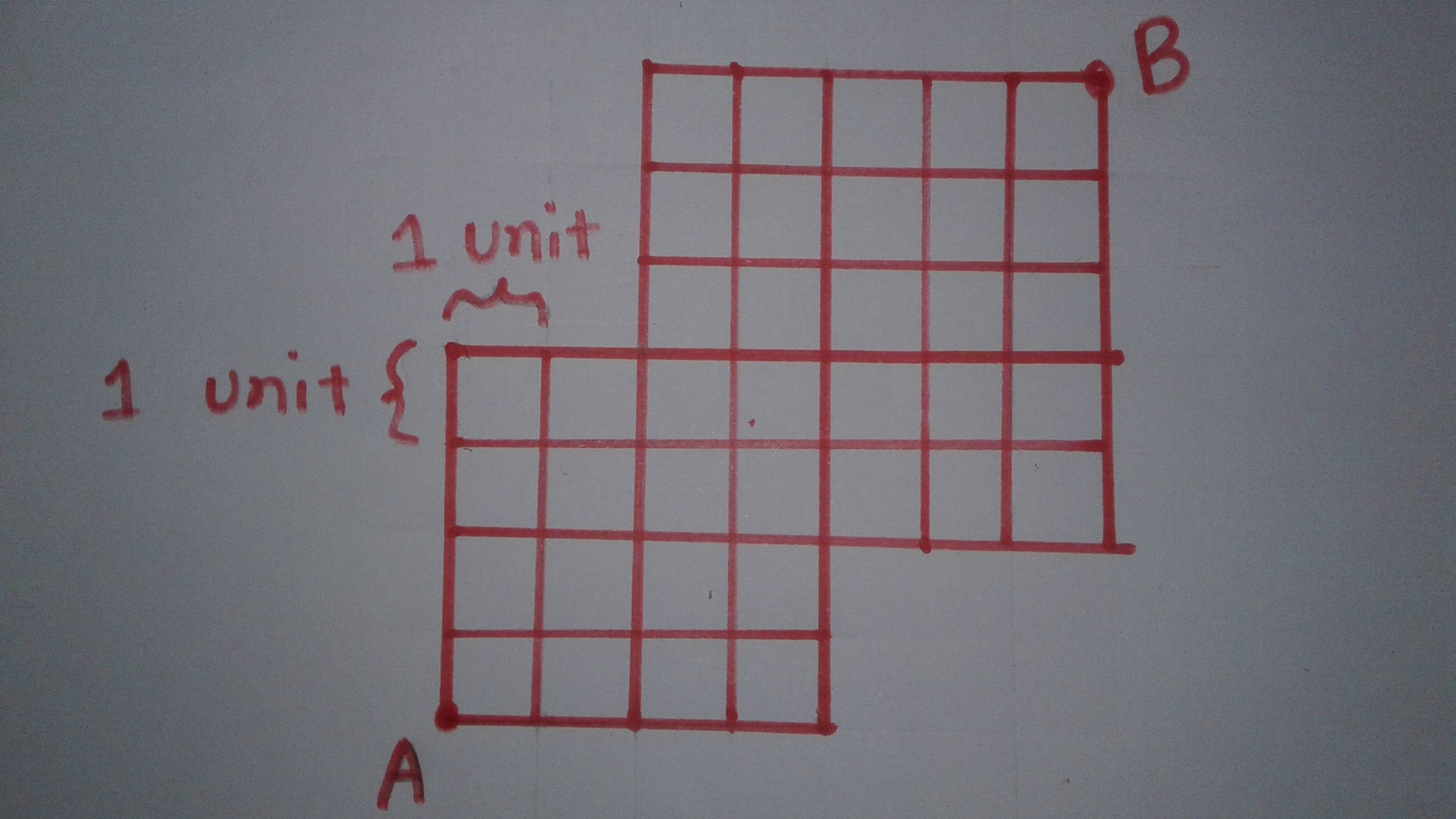
The answer is 3080.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Every path from A to B has to go through one of three points, call them P, Q and R, as shown below on the left.
Let's call a network of paths, like the one from A to P or from P to B, a "complete rectangle". If such a network consists of m steps to the right, and n steps upwards, the number of shortest paths would be m ! n ! ( m + n ) ! = ( m m + n ) . One way to see this is to label each step to the right as R, and every step upward as U; then each path is a permutation of m R's and n U's.
Then the number of paths from A to B that go through P is ( 2 6 ) ( 3 8 ) ; the number of paths from A to B that go through Q is ( 3 6 ) ( 4 8 ) ; and the number of paths from A to B that go through R is again ( 2 6 ) ( 3 8 ) . Then the total number of paths is
( 2 6 ) ( 3 8 ) + ( 3 6 ) ( 4 8 ) + ( 2 6 ) ( 3 8 ) = 3 0 8 0