Finding the Side Length
In triangle A B C , we have ∠ B C A = 3 ∠ C A B , B C = 3 4 3 and A B = 5 0 4 . What is A C ?
The answer is 253.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Let α = ∠ C A B . Since 0 < α < 1 8 0 ∘ , we have 0 < sin α ≤ 1 . By Sine Rule, we get that 3 4 3 sin α = 5 0 4 sin ( 3 α ) = A B sin ( 1 8 0 − 4 α ) .
By the triple-angle formula, we know that sin ( 3 α ) = 3 sin α − 4 sin 3 α . Substitution into the first equality yields 3 4 3 sin α = 5 0 4 3 sin α − 4 sin 3 α , which simplifies to 1 9 6 sin 3 α − 7 5 sin α = 0 , so sin α = 1 4 5 3 , and cos α = 1 4 1 1 . (The other 2 roots 0 and − 1 4 5 3 are rejected because of our condition on sin α .
By the double-angle formula, we know that sin ( 1 8 0 ∘ − 4 α ) = sin ( 4 α ) = 2 sin ( 2 α ) cos ( 2 α ) = 4 sin α cos α ( 1 − 2 sin 2 α ) . Substituting into the second equality yields 3 4 3 sin α = A B 4 sin α cos α ( 1 − 2 sin 2 α ) , which simplifies to A B = 3 4 3 × 4 cos α ( 1 − 2 sin 2 α ) . Substituting the values for sin α and cos α above will give A B = 2 5 3 .
Let ∠ C A B = α , so that ∠ B C A = 3 α . Construct the point D on A B such that ∠ A C D = α . Note that this creates the isosceles triangle A C D . We also have ∠ C D B = ∠ D A C + ∠ A C D = α + α = 2 α = ∠ B C D , so triangle C D B is isosceles as well. This means B D = B C = 3 4 3 , and so C D = A D = A B − B D = 5 0 4 − 3 4 3 = 1 6 1 .
Now by dropping the perpendicular of D to A C we see that A C = 2 ( 1 6 1 cos α ) = 3 2 2 cos α . Hence we are done if we can find cos α .
We consider triangle C D B since we know all its side lengths and angles. By the law of sines, sin ∠ C D B B C = sin ∠ D B C C D ⟹ sin 2 α 3 4 3 = sin ( 1 8 0 ∘ − 4 α ) 1 6 1 Using trig identities, sin ( 1 8 0 ∘ − 4 α ) = sin 4 α = 2 sin 2 α cos 2 α , so after some rearranging the equation becomes cos 2 α = 9 8 2 3 . By the half angle formula for cosine, we have cos α = ± 2 cos 2 α + 1 . But since α and 3 α are angles of triangle A B C , we know α + 3 α < 1 8 0 ∘ , or α < 4 5 ∘ . Therefore, cos α is positive and cos α = 2 cos 2 α + 1 = 1 4 1 1 . The length we seek is A C = 3 2 2 cos α = 2 5 3 .
DC=CE=sqrt(EB ED)=sqrt(343 (504+343))=539, DA=DB DE/DC=504 (504+343)/539=792, AC=AD-DC=792-539=253
Let ∠ C A B = α . Then ∠ B C A = 3 α and ∠ A B C = 1 8 0 − 4 α .
By sine rule, we have s i n α 3 4 3 = s i n 3 α 5 0 4 = s i n ( 1 8 0 − 4 α ) A C = s i n 4 α A C , s i n α = 0 .
From s i n α 3 4 3 = s i n 3 α 5 0 4 , we have s i n α s i n 3 α = 3 4 3 5 0 4 − ( 1 ) .
Then, note that
s i n 3 α = s i n ( 2 α + α )
= s i n 2 α c o s α + c o s 2 α s i n α
= 2 s i n α c o s 2 α + s i n α ( 1 − 2 s i n 2 α )
= 2 s i n α ( 1 − s i n 2 α ) + s i n α ( 1 − 2 s i n 2 α )
= 2 s i n α − 2 s i n 3 α + s i n α − 2 s i n 3 α
= 3 s i n α − 4 s i n 3 α
Combining it with ( 1 ) , we obtain 3 − 4 s i n 2 α = 3 4 3 5 0 4 ⇒ s i n 2 α = 1 9 6 7 5
From s i n α 3 4 3 = s i n 4 α A C , we have s i n α s i n 4 α = 3 4 3 A C ⇒ A C = 3 4 3 × s i n α s i n 4 α .
Computing s i n α s i n 4 α , we get
s i n α s i n 4 α = s i n α 2 s i n 2 α c o s 2 α
= s i n α 4 s i n α c o s α c o s 2 α
= 4 c o s α c o s 2 α
= 4 ( 1 − s i n 2 α ) ( 1 − 2 s i n 2 α )
(since 0 ∘ < ∠ B A C + ∠ B C A = 4 α < 1 8 0 ∘ ⇒ 0 ∘ < α < 4 5 ∘ )
Thus,
A C = 3 4 3 × 4 × ( 1 − s i n 2 α ) ( 1 − 2 s i n 2 α )
= 1 3 7 2 ( 1 − 1 9 6 7 5 ) ( 1 − 2 ( 1 9 6 7 5 ) )
= 1 3 7 2 ( 1 9 6 1 2 1 ) ( 9 8 2 3 )
= 1 3 7 2 ( 1 4 1 1 ) ( 9 8 2 3 )
= 2 5 3
By Law of Sines we have sin(3x)/sinx=504/343=72/49. Expanding sin(3x) as 3sin(x)cos^2(x)-sin^3(x), we can substitute cos^2(x)=1-sin^2(x) and get sin(x)=5\sqrt{3}/14. Now since <B=180-4x, sinB=sin4x, so by Law of Sines again, we have AC/343=sin(4x)/sinx.
Since sin(4x)=2sinxcosxcos(2x), we have 2 343 cos(x)cos(2x)=AC. We can easily find cos(x)=\sqrt{1-sin^2(x)). The answer is 253.
Let angle BCA be 3x, therefore, angle BAC is x.
From the sine law, we know that sin3x/504 = sinx/343. From the trigonometric identities, we know that sin3x = 3sinx - 4sin^3x.
Therefore (3sinx - 4sin^3x)/504 = sinx/343.
Expanding this we get sinx(sin^2x - 525/1372) = 0 Here, we have two cases, sinx=0 or sin^2x - 525/1372=0.
We know that sinx=0 is impossible because angle x would be 90 and the sum of the interior angles of the triangles will be larger than 180.
If sin^2x - 525/1372=0 then sinx = sqrt (525/1372) and x = arcsin (sqrt (525/1372).
Let angle ABC=y
To use the cosine law, we need to know angle y, and knowing that the sum of the angles in a triangle sums up to 180, we get the equation,
So,y=180-4(arcsin (sqrt (525/1372)))
Therefore, from the cosine law, we know that AC^2 = 504^2 + 343^2 - 2(504)(343)cosy
After subbing in y, we will get AC^2 = 64009
Therefore AC = 253
Suppose, ∠BAC = x then ∠BCA = 3x and since the sum of all angles of the triangle is 180 degress, therefore ∠ABC = (180-4x).
Now, applying the sine rule for a traingle:
sin x / 343 = sin 3x / 504 = sin (180-4x) / (length of AC) Solve the first two part of the equation to get the value of x and then solve the third part of the equation with any one of the other parts to determine the length of AC.
Calling angle BCA x, Using the law of sines and the expansions for sin 3x and sin 4x, which is equivalent to sin CBA, AC can be found with some computation.
Let B C = a , C A = b , A B = c . By using sine rule, we have sin A a = sin B b = sin C c . Since C = 3 A , we have sin C = 3 sin A − 4 sin 3 A . Hence, 5 0 4 sin A = 3 4 3 ( 3 sin A − 4 sin 3 A ) ⇔ sin A = 1 4 5 3 (since 0 < sin A < 1 ). Then sin B = sin ( 1 8 0 ∘ − 4 A ) = sin 4 A = 4 sin A cos A cos 2 A = 4 8 0 2 1 2 6 5 3 . Therefore, b = 1 4 5 3 3 4 3 ⋅ 4 8 0 2 1 2 6 5 3 = 2 5 3 .
Let ∠ B A C = θ , so we have ∠ A C B = 3 θ . Place D on A B such that ∠ D C A = ∠ D A C = θ . Hence D A C is isosceles and we have ∠ D C B = 3 θ − θ = 2 θ . Also ∠ B D C = ∠ D A C + ∠ D C A = 2 ∠ D A C = 2 θ . Hence B D C is also isosceles.
Thus D B = B C = 3 4 3 and D C = D A = 5 0 4 − 3 4 3 = 1 6 1 . Applying the cosine rule to triangle B D C , we have cos ∠ A B C = 2 × 3 4 3 × 3 4 3 3 4 3 2 + 3 4 3 2 − 1 6 1 2 . Applying the cosine rule to triangle A B C , we have cos ∠ A B C = 2 × 5 0 4 × 3 4 3 5 0 4 2 + 3 4 3 2 − A C 2 . Equating these expressions, we solve for A C (and use the fact that 5 0 4 = 3 4 3 + 1 6 1 ) to obtain
A C 2 = ( 3 4 3 + 1 6 1 ) 2 + 3 4 3 2 + ( 1 6 1 2 − 2 × 3 4 3 2 ) ( 3 4 3 3 4 3 + 1 6 1 ) = 2 × 3 4 3 2 + 2 × 3 4 3 × 1 6 1 + 1 6 1 2 + 1 6 1 2 + 3 4 3 1 6 1 3 − 2 × 3 4 3 2 − 2 × 3 4 3 × 1 6 1 = 2 × 1 6 1 2 + 3 4 3 1 6 1 3 = 7 3 1 6 1 2 ( 2 × 3 4 3 + 1 6 1 ) = 2 3 2 ( 1 2 1 ) = 2 5 3 2
Therefore A C = 2 5 3 .
by sine law we get (3sinx-4sin^3x)/504=sinx/343 solving x from there then 180-4x .next we take cos of that value 2 343 504 and subtract it from 504 504+343*343. we take the squareroot of that no. and it is the value of AC.
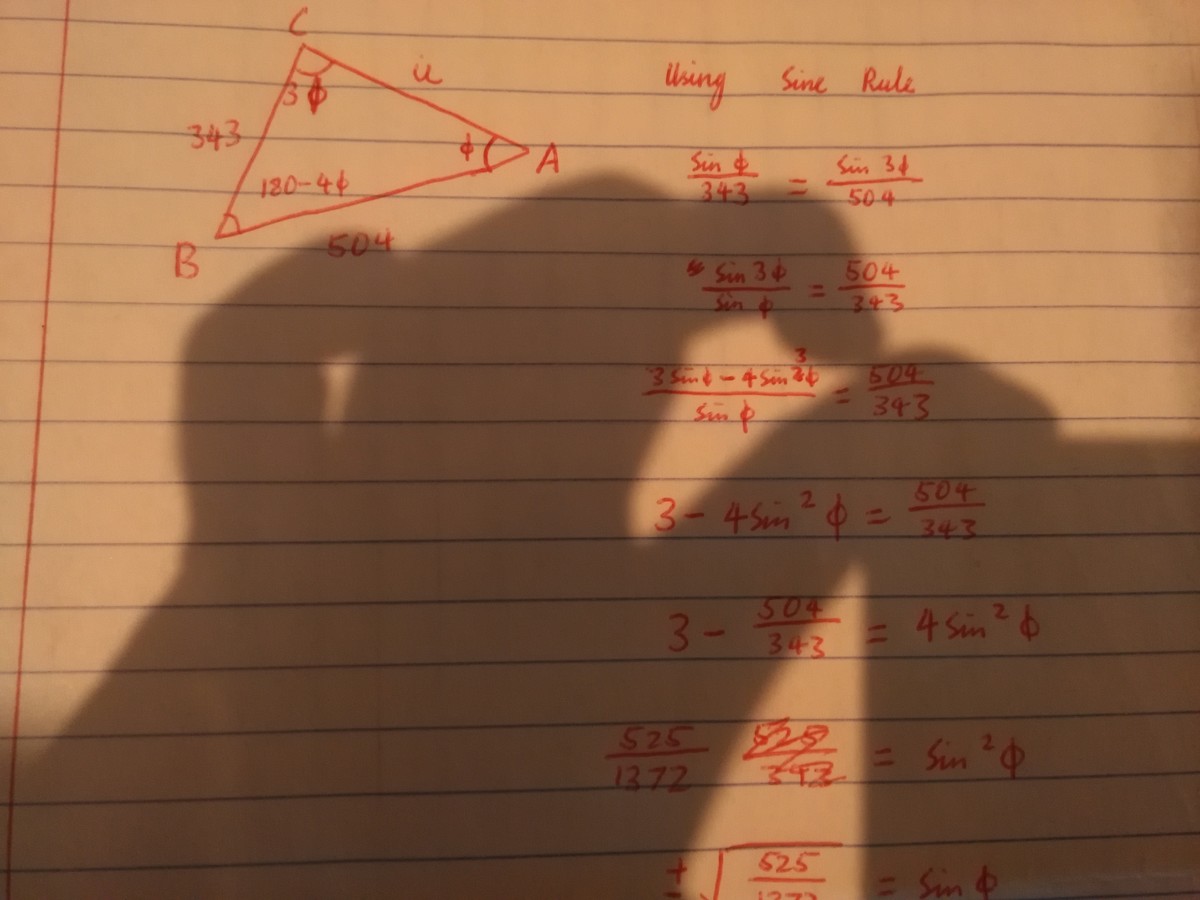

Firstly, draw C D and C E which trisect angle B C A , and D and E are on line A B with D nearer to A . Let ∠ C A B = α , so ∠ B C E = ∠ E C D = ∠ D C A = α . Then, we can get triangle C E B is similar to triangle A C B since they are α − 3 α − 1 8 0 ∘ − 4 α triangles. Also, triangle D C E is similar to triangle C A E , since they are α − 2 α − 1 8 0 ∘ − 3 α triangles.
Since C B D is an isosceles triangle, C B = B D = 3 4 3 and A D = D C = 5 0 4 − 3 4 3 = 1 6 1 . Since triangle C E B is similar to triangle A C B , we get B E : B C = B C : B A which gives B E = 7 2 1 6 8 0 7 and D E = 3 4 3 − B E = 7 2 7 8 8 9 . Since triangle D C E is similar to triangle C A E , we get D E : C E = C E : A E which gives C E = 7 2 1 2 3 9 7 . Also, C D : A C = D E : C E which gives 1 6 1 : A C = 7 2 7 8 8 9 : 7 2 1 2 3 9 7 . Solving it we get A C = 2 5 3 and we are done.