Finite Quantum Well (Part 2)

Classical Mechanics Level 4

This is a continuation of Part 1 .

Assuming that $E$ takes its lowest (and only) allowable value, what is the probability of observing the particle outside the well in the region $|x| > 1$ ?

Note: The constraints from the previous problem apply here too

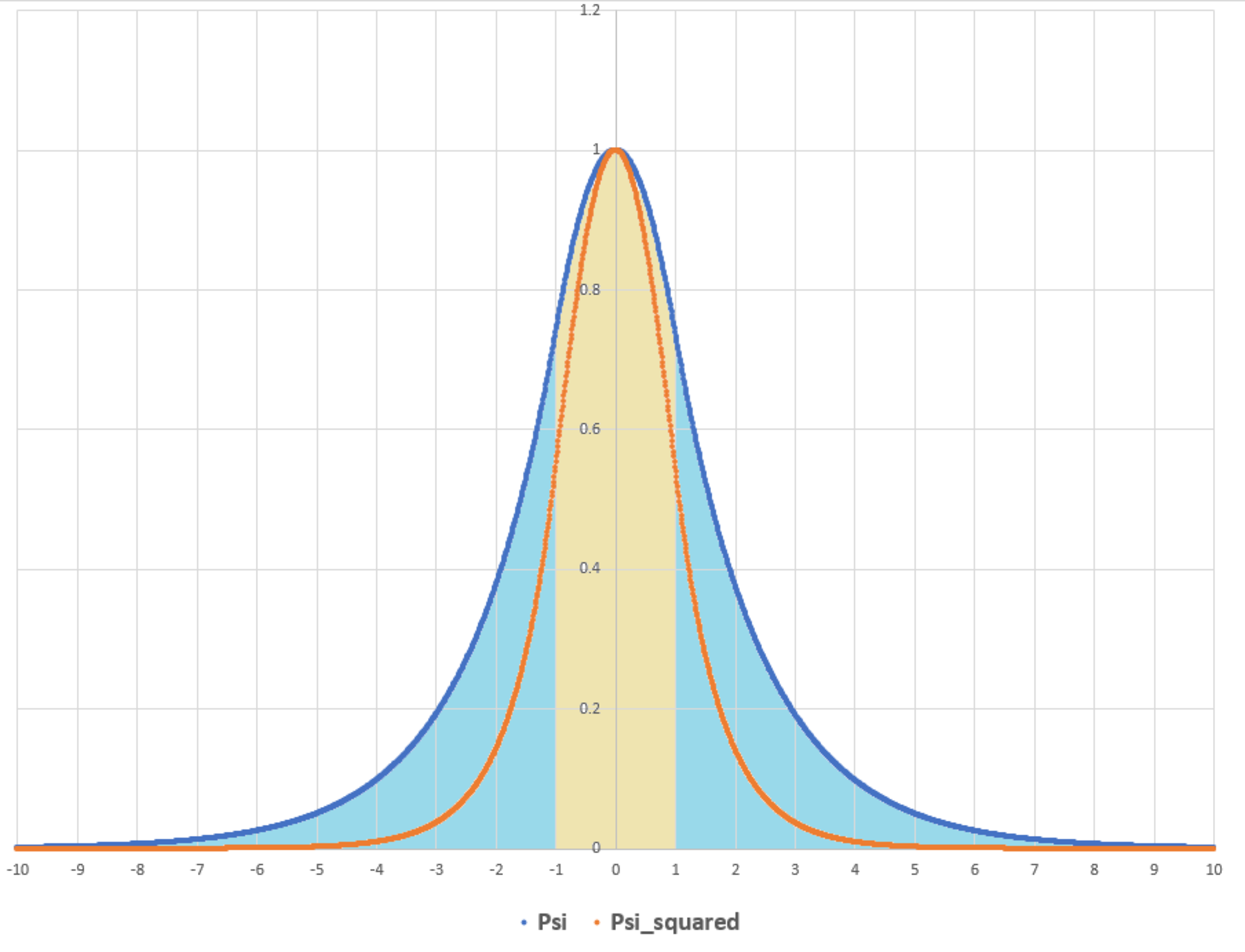
The answer is 0.33.

1 solution

Karan Chatrath
Sep 22, 2019

Since the solution is even, consider only the right half of the solution. COnsidering both halves of the solution will yield the same result. Assuming boundary conditions of $\psi(0) = 1$ and $\dot{\psi}(0) = 0$ , we have:

$\psi(x) = \cos(\sqrt{E}x) \ ;\ x\le1$ $\psi(x) = Ae^{\sqrt{1-E}x} \ ;\ x>1$

Now the value of $E$ is known from the previous problem and the value of $A$ can be obtained by ensuring that the wave function is continuous at $x =1$ . This gives:

$A = \cos(\sqrt{E})e^{\sqrt{1-E}}$

Now, the required probability can be computed as such:

$P(\mid x \mid >1 ) = \frac{\int_{1}^{\infty}\psi^2(x)dx}{\int_{0}^{\infty}\psi^2(x)dx}$

The evaluation is a pretty standard process. The answer comes out to be:

$\boxed{P(\mid x \mid >1 ) \approx 0.33}$

Just do $1-\int_{-1}^{1} {\psi(x)}^2 dx=1-\int_{-1}^{1} (Cos(√Ex))² dx$ which is equals to $0.33...$ for minimum allowed energy $E=0.5462486$ .

Alapan Das - 1 year, 8 months ago

Thank you for your comment. I understand your approach. However, there are two errors here. One is that the integral you have shown does not evaluate to approx. 0.66. Secondly, probability density functions are the absolute value squared of the normalised wave function and not of the un-normalised wave function itself. You have used the square of the un-normalised wave function here.

Karan Chatrath - 1 year, 8 months ago

I wrote ${\psi(x)}²$ because here $\psi$ is purely real. So, ${|\psi(x)|}²={\psi(x)}²$ .

Alapan Das - 1 year, 8 months ago

I understand this bit. This isn't the point I'm making, though. I request you to re-check your working as the integral you have shown does not evaluate to the correct answer.

Karan Chatrath - 1 year, 8 months ago

Yes the answer comes 1-0.6737...≈0.33.

Alapan Das - 1 year, 8 months ago

I see that your first comment is edited. Unfortunately, the answer is still not obtained despite the correction. The integral: $\int_{-1}^{1} \cos^2(x\sqrt{E})dx = 1.673$

It does not evaluate to 0.673. I request you to re-read my initial comment.

Karan Chatrath - 1 year, 8 months ago

Finite Quantum Well (Part 2)

The answer is 0.33.

1 solution

0 pending reports