Finite resistance
Consider the following model (see the figure) of a long cable connecting the points A and B. Each resistor in the figure has resistance
R
=
1
Ω
. Determine the equivalent resistance
R
A
B
in Ohms
. Assume the number of resistors to be infinite.
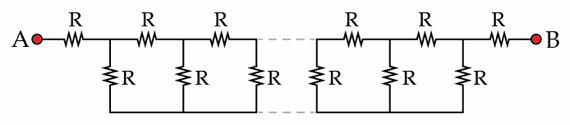
The answer is 3.24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice and short solution.. But should'nt the equation have been r 2 + 2 r − 4 = 0 ??
Please correct me if i am wrong.
Log in to reply
oh you are right i have dona mistake there. sorry
Suppose that there are n nodes between A and B in the top row. All the nodes in the bottom row can be collapsed to a single node with n 1 Ω resistors leading from it.
Suppose that the voltages at A , the n nodes between A and B and B are V 0 , V 1 ,..., V n , V n + 1 , and that the voltage at the (now single) bottom node is 0 . Kirchoff's Laws tell us that V j + 1 − 3 V j + V j − 1 ∑ j = 1 n V j = = 0 1 ≤ j ≤ n 0 Suppose that λ > 1 > μ > 0 are the roots of the quadratic equation X 2 − 3 X + 1 = 0 . Then we deduce, solving the recurrence relation, that V j = A λ j + B μ j 1 ≤ j ≤ n + 1 and the last condition tells us that 0 = = A λ − 1 λ ( λ n − 1 ) + B μ − 1 μ ( μ n − 1 ) A ( λ − 1 ) ( λ n − 1 ) + B ( 1 − μ ) ( 1 − μ n ) so that A = − C ( 1 − μ ) ( 1 − μ n ) B = C ( λ − 1 ) ( λ n − 1 ) and hence, for 0 ≤ j ≤ n + 1 , V j = C [ ( λ − 1 ) ( λ n − 1 ) μ j − ( 1 − μ ) ( 1 − μ n ) λ j ] The potential difference across the circuit is V 0 − V n + 1 , and the current through the circuit is V 0 − V 1 . Thus the effective resistance of this circuit is R n = V 0 − V 1 V 0 − V n + 1 = λ n − μ n 2 [ ( λ − 1 ) λ n − ( λ − μ ) + ( 1 − μ ) μ n ] Since λ > 1 > μ > 0 , it is clear that n → ∞ lim R n = 2 ( λ − 1 ) and so the effective resistance of the infinite circuit is 2 ( λ − 1 ) = 1 + 5 .
Its really a great solution sir. The way u have solved. thank you for the wonderful solution.
it's a little hard to explain without figures.(so please try to visualize)
let us take a triangle loop which has a res. on each arm(this is the middle of the infinite series given)
now, the next connections are as follows: the base extends on both sides with one res. on each side. to these, a res. each are connected from the top vertex of the prev. triangle and thus a new triangle is formed.
this way the series extends infinitely finally terminating at A and B.(notice that AB does not form any triangle)
now, if you could imagine the whole picture, you could say by symmetry that the current through one triangle arm crosses the vertex and goes in the other arm of the same triangle.so, we could say that the common joint(the common top vertex shared by all triangles) is a pseudo joint and thus all the triangles act as if there top vertices are not connected at all( this technique is correct and can be proved easily for simpler but similar circuits and is often used in solving such circuits).
so,as all the triangles are separated now, let the equivalent res. be x. as series is infinite,the equivalent res. just inside the biggest enclosing triangle can also be said to be x.
therefore, ((2R)x/(x+2R)) + 2R = x
solving the quadratic so formed,
x=3.24
we can consider the equivalent circuit to be as show in the diagram Alt text
Alt text
the reason for this new circuit is that since there are no resistors connected in the bottom portion when separated it doesnt make a difference
considering the resistance of the infinite sequence to be r the equation will be
2 R + r 1 + 2 R 1 = r 1
We know that, R = 1 Ω
⇒ r 2 + 2 r − 4 = 0
∴ on solving for r we get r = 5 − 1 ≈ 1 . 2 3 6 0
Therefore the equivalent resistance will be R e q i v = 2 R + r = 2 + 1 . 2 3 6 0 ≈ 3 . 2 4