Finite State Machines 2
Computer Science
Level
1
Which string cannot be generated by the finite state machine below?
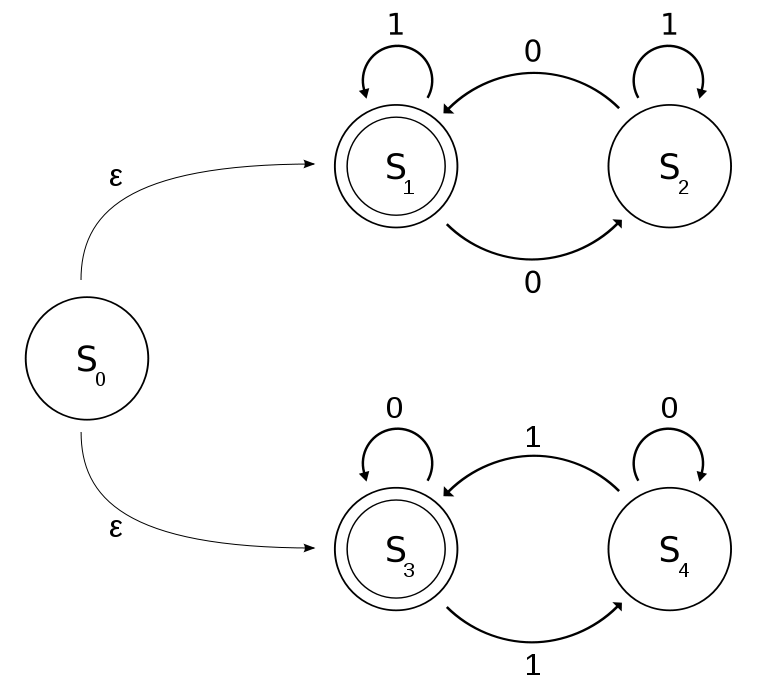
1
01001
1011101
1000
0
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The top finite state automaton will always reach an end state when the remainder of the total number of 0's when divided by 2 is 0, the number of 0's will always be a multiple of two.
The bottom automaton can in fact yield an odd number of 0's, however it will always have an even number of 1's.
The string which matches neither of these criteria is 1000, as it has both an odd number of 1's and 0's. Therefore it can not be generated by this automaton.