Firing a Cannon
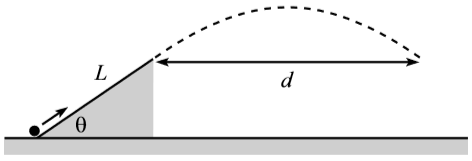
A cannon, when aimed vertically, is observed to fire a ball to a maximum height of Another ball is then fired with this same speed, but with the cannon now aimed up along a plane of length inclined at an angle Neglect air resistance and friction on the inclined plane.
What should be, so that the ball travels the largest horizontal distance, by the time it returns to the height of the top of the plane?
If the answer can be written as find the value of
The answer is 0.434259.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the initial velocity of the ball be u . Then by the conservation of energy 2 1 m u 2 = m g L . Now consider the ball moving on the inclined plane. Let the velocity when the ball emerges from the plane be v . Then by the conservation of energy again, we have:
m g L sin θ + 2 1 m v 2 2 1 m u 2 sin θ + 2 1 m v 2 = 2 1 m u 2 = 2 1 m u 2 Note that 2 1 m u 2 = m g L
⟹ v 2 = u 2 ( 1 − sin θ )
Now we know that the range d of the trajectory is given by:
d = g v 2 sin ( 2 θ ) = g u 2 ( 1 − sin θ ) sin ( 2 θ ) Since v 2 = u 2 ( 1 − sin θ )
We note that d is maximum when f ( θ ) = ( 1 − sin θ ) sin ( 2 θ ) is maximum.
f ′ ( θ ) = 2 ( 1 − sin θ ) cos ( 2 θ ) − cos θ sin ( 2 θ ) = 2 ( 1 − sin θ ) ( 1 − 2 sin 2 θ ) − 2 sin θ ( 1 − sin 2 θ ) = 2 ( 1 − sin θ ) ( 1 − 2 sin 2 θ − sin θ − sin 2 θ ) = 2 ( 1 − sin θ ) ( 1 − sin θ − 3 sin 2 θ )
Putting f ′ ( θ ) = 0 to find the extrema, we have
⎩ ⎪ ⎨ ⎪ ⎧ sin θ = 1 ⟹ θ = 2 π sin θ = x = 6 1 3 − 1 ≈ 0 . 4 3 4 when d = 0 , the minimum when d is maximum