Firing across

Classical Mechanics Level 3

A hollow cylinder with radius r can rotate freely and frictionless about its (vertical) axis. The axis does not extend in the inside of the cylinder. On the inside of the wall of the cylinder, there is a small gun with a bullet in it. The gun is mounted at right angles to the wall of the cylinder, directed towards its centre. At the opposite wall there is a patch of putty that will catch the bullet. Gravity and air resistance do not play a role in this thought experiment.

The bullet has mass M. The cylinder, gun and putty together also have mass M. The mass of the gun and putty are such that they balance and their sizes can be ignored with respect to r. 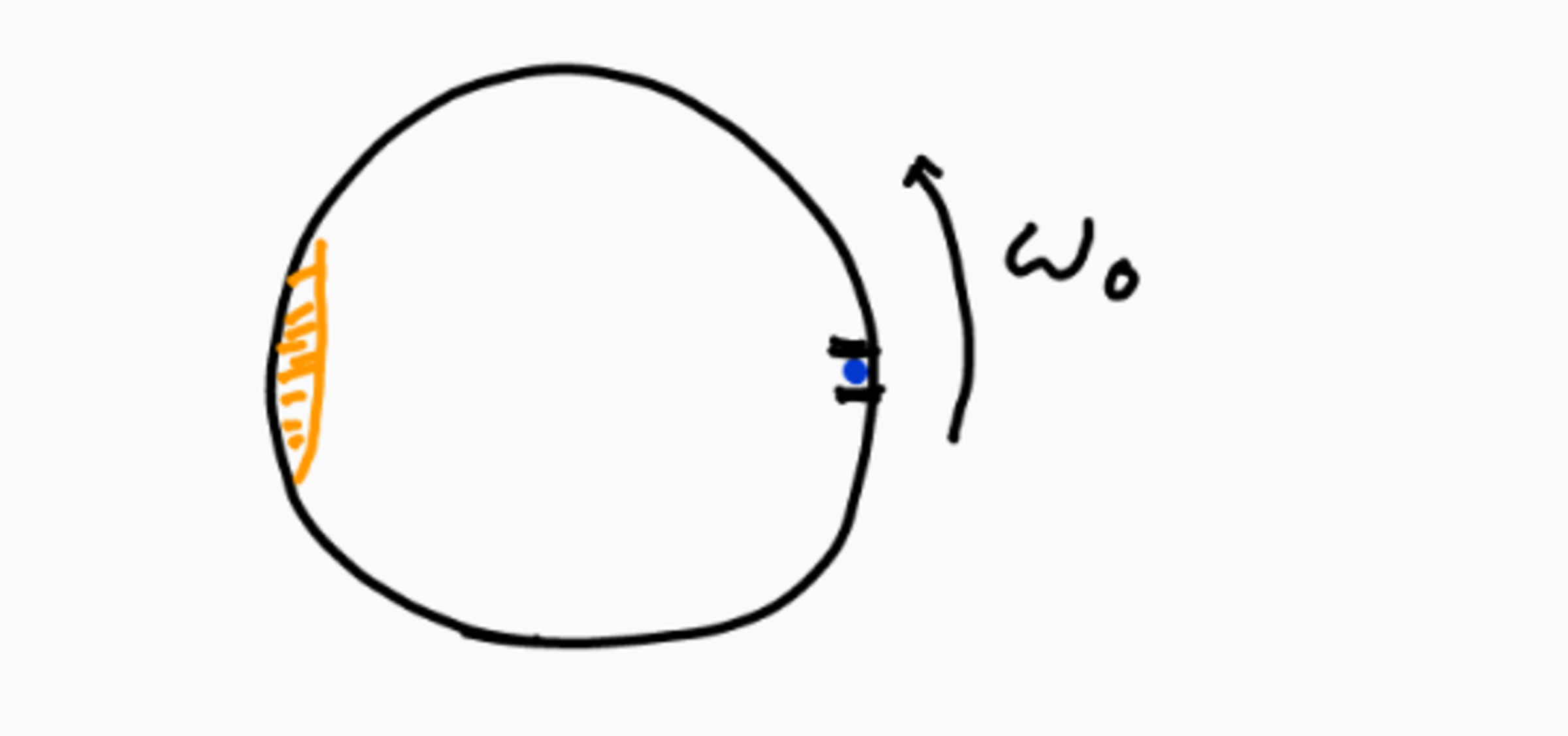Schematic top view of the setup, at moment of ignition

The cylinder rotates slowly counterclockwise with angular velocity ω 0 ω_0 and at the moment the gun is at the right hand side, it fires. The explosion adds a momentum to the bullet that is directed towards the axis of the cylinder. The bullet moves with speed v > > ω 0 r v>>ω_0r .

After the bullet has landed in the putty, what is the angular velocity of the cylinder?

A. ω 0 ω_0 , because of conservation of angular momentum.

B. It will come to rest, because apart from the leftward momentum m v mv the bullet gets from the explosion, it also has the also a tangential ('y-direction') component m ω 0 r mω_0r . At the left side of the cylinder this y-component of the motion will push the cylinder clockwise and thus stop it.

C. The bullet will slow the rotation down when it lands in the putty, but it will not stop the rotation entirely.

D. ω 0 ω_0 . Because the bullet was shot when rotating, it will keep its rotational motion, going right through the centre and landing at right angles to the wall. It therefore does not transfer any angular momentum.

E. It is incorrect to state that gravity or air resistance do not play a role.

Pick the right answer and describe in detail what is wrong with the other options.

A B C D E

K T by K T , 55, Netherlands

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

K T
Dec 15, 2020

A. Correct. There are no external torques on the cylinder or its contents. The angular velocity just has to be unchanged because mass distribution as a function of radius is the same as before and conservation of angular momentum is a universal law of physics.

B. Wrong. While it is true that the bullet has a tangential component ω 0 r ω_0r and therefore has a nonzero velocity in the y-direction, it would transfer negative angular momentum m ω 0 r mω_0r to the cylinder, if it landed on the exact opposite spot . But because of this velocity component it will also land 'above' the middle (i.e. with a positive y-coordinate). It turns out that its momentum is directed at right angles to the motion of the putty, and therefore does not accelerate nor decelerate the circular motion. This can be seen by symmetry. The bullet trajectory is a straight line, not exactly a diameter, but a chord passing above the centre. The angle and speed with which it leaves the gun are identical to the angle and speed with which it lands on the putty. With respect to the axis, the bullet has angular momentum ω 0 r M ω_0rM at all times, and so has the cylinder including gun and putty.

To consider this quantitatively (in 1st-order approximation) when v > > r v>>r : The bullet's velocity is v x , b = − v v_{x,b}=-v v y , b = ω 0 r v_{y,b}=ω_0r It has moved in direction v y , b / v x , b = − ω 0 r / v v_{y,b}/v_{x,b} =-ω_0r/v when it hits the cylinder wall having traveled over Δ x = − 2 r Δx=-2r . So the place of impact is therefore x = − r , y = 2 ω 0 r 2 / v x=-r, y=2ω_0r^2/v . At that point the motion of the putty is v x , p = − ω 0 y = − 2 ω 0 2 r 2 / v v_{x,p}=-ω_0y = -2ω_0^2r^2/v v y , p = ω 0 x = − ω 0 r v_{y,p}=ω_0x=-ω_0r

The velocitity of the bullet can be decomposed into a tangential and a radial component. v ⃗ t a n g e n t i a l = v b ⃗ ⋅ v p ⃗ ∣ v p ⃗ ∣ 2 v p ⃗ = 2 ω 0 2 r 2 − ω 0 2 r 2 ( ω 0 r ) 2 v p ⃗ = v p ⃗ \vec{v}_{tangential}=\frac{\vec{v_{b}} \cdot \vec{v_p}}{|\vec{v_p}|^2 } \vec{v_p}=\frac{2ω_0^2r^2-ω_0^2r^2}{ (ω_0r)^2} \vec{v_p}= \vec{v_p} The tangential component of the bullet's velocity is indeed equal to the velocity of the putty, so that there is only a radial force during impact.

C. See explanation at B.

D. It is incorrect to assume that in a rotating frame the normal laws of physics will hold. For example, in a rotating frame, the bullet has a curved trajectory, and we would need to invent apparent forces (centifugal and coriolis forces) to describe it.

E. There is no reason why the thought experiment couldn't work in space, without air or gravity. So the paradox cannot be attributed to (or solved with) friction or gravity effects.

1 Helpful 1 Interesting 1 Brilliant 0 Confused

Conceptual Comment: Regardless of the masses or the bullet speed or the orientation of the gun, the easiest way to see that the final angular velocity will be ω 0 \omega_0 is using conservation of angular momentum (choice A).

However, in this case (gun aimed at the center of the circle with a high speed bullet), almost everything said in choice D is also true. Due to the position of the gun, the forces exerted between the bullet and cylinder are radial at both the launch and the impact, so the two never affect each other's angular momentum. You made this point when discussing choice B. Usually, we would say that the angular momentum of the system is conserved throughout. Well, in this case, the angular momentum of each individual object is conserved throughout! And although the bullet misses the center of the circle and does not hit the far wall at a right angle, both these statements are nearly true when v > > ω 0 r v >> \omega_0 r .

Mathematical Comment: The y y -component of the putty velocity is half what you said because the x x -coordinate should be measured from the center of the circle. v y , p = ω 0 ( x p u t t y − x c e n t e r ) = ω 0 ( − 2 r − ( − r ) ) = − ω 0 r v_{y,p} = \omega_0 (x_{putty} - x_{center}) = \omega_0 (-2r - (-r)) = - \omega_0 r .

Matthew Feig - 5 months, 3 weeks ago

Thank you for helping improve the answer, you thought well about it. I agree with your mathematical comment and corrected the last part of the explanation in B.

About D though we do not entirely agree. The given reasoning is unsound. Free bodies do not 'keep their rotational motion' about any point other than their own centre of gravity, and the bullet does not go 'right through the centre', nor does it 'land at right angles to the wall'. Although you are right it almost does for the latter two, that leaves unclear which things we can or can't ignore to get the answer right for this problem. After all, half the total angular momentum is actually in the bullet, and saying that it goes through the centre would sweep that under the carpet. The given answer happens to be correct here, but I consider that a coincidence; similar reasoning would lead to the wrong answer in many problems involving rotation.

K T - 5 months, 3 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...