First Quadrant Portion of an Ellipse
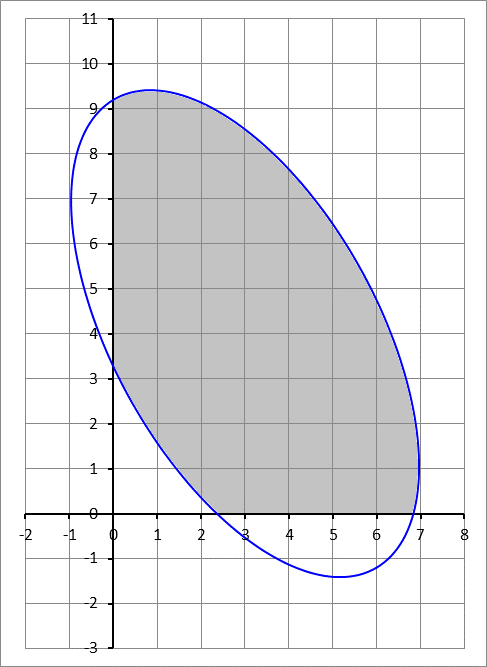
An ellipse is centered at . It has a semi-minor axis of 3 units, and a semi-major axis of 6 units. Originally, the minor axis is horizontal and the major axis is vertical. The ellipse is rotated counter-clockwise about its center by an angle of , resulting in the ellipse shown in the figure above.
Find the area of the portion of the ellipse that lies in the first quadrant (the shaded region). Round your answer to three decimal places.
Hint : Use the special form of Green’s Theorem used for finding areas.
The answer is 48.280.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The ellipse can be represented in parametric form as
r ( t ) = r c + v 1 cos ( t ) + v 2 sin ( t )
where r c = [ 3 , 4 , 0 ] T , v 1 = R [ 3 , 0 , 0 ] T , v 2 = R [ 0 , 6 , 0 ] T
with R being the rotation matrix by 3 0 ∘ or π / 6
That is,
R = ⎣ ⎡ cos 6 π sin 6 π 0 − sin 6 π cos 6 π 0 0 0 1 ⎦ ⎤
Based on Green's Theorem, one can derive the following formula for the area,
A = 2 1 ∥ ∮ C r ( t ) × d t d r d t ∥
The rest is calculating the intervals of the parameter t where r ( t ) lies in the first quadrant, i.e. has positive x ( t ) , and y ( t ) , and performing the above integral. There are two intervals in this case which satisfy this condition, one corresponds to the upper and right part of the ellipse, and the other to the lower part. The other segments of the boundary are along the x-axis and y-axis, and their contribution to the above integral is zero.