This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
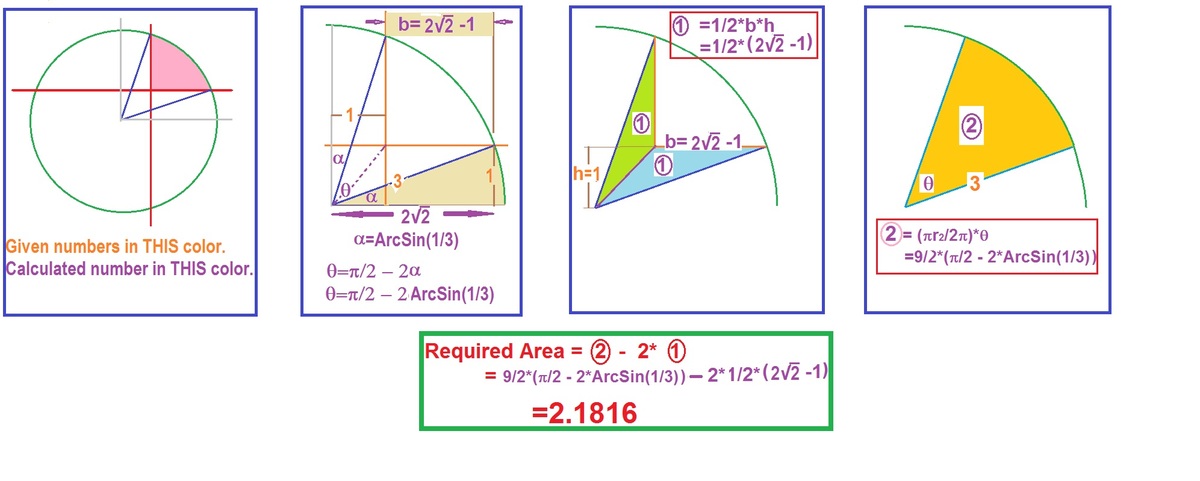
Some how, with the 2,1816 in the answer , it seems I pressed the wrong button !! Any way my solution.
Part of x-axis is the chord at a distance of 1. x-axis cuts the circle at P. Let O be (-1,-1).
PO makes an angle of ArcSin(1/3) with horizontal. Because of symmetry, same angle is made with y-axis. So the sector makes an angle of ,
2
1
∗
π
−
2
∗
A
r
c
S
i
n
(
3
1
)
.
So the desired area is the sector area - the unwanted two triangular area covering it on the two sides.
The base 'b' of the triangular area with x-axis =Half chord - distance of origin from y-axis. Because origin is the corner of the colored area.
b
=
3
2
−
1
2
−
1
=
2
2
−
1
.
a
n
d
h
e
i
g
h
t
h
=
1
.
∴
T
h
e
t
w
o
t
r
i
a
n
g
u
l
a
r
a
r
e
a
s
=
2
∗
2
1
∗
(
2
2
∗
1
−
1
)
=
2
2
−
1
.
.
.
.
.
.
.
.
.
(
1
)
S
e
c
t
o
r
a
r
e
a
=
2
π
π
∗
3
2
∗
{
2
1
∗
π
−
2
∗
A
r
c
S
i
n
(
3
1
)
}
.
.
.
.
.
.
.
.
(
2
)
R
e
q
u
i
r
e
d
A
r
e
a
=
(
2
)
−
(
1
)
=
2
.
1
8
1
6
.
Log in to reply
A picture would greatly help your solution ;)
Log in to reply
I have posted a sketch. Last time I did not have the time for a sketch. Thank you.
Great approach that deals with the tricky curvy part using sectors :)
The equation of the circle in parametric form is given by
r ( t ) = r c + v 1 cos t + v 2 sin t
where r c = [ − 1 , − 1 , 0 ] T , v 1 = [ 3 , 0 , 0 ] T , v 2 = [ 0 , 3 , 0 ]
We need to find values of t, that correspond to the intersection of the circle with the positive x-axis, and the positive y-axis. Using simple geometry, we immediately find that
t 1 = sin − 1 3 1 = 0 . 3 3 9 8 3 6 9 0 9 5 and t 2 = 2 π − sin − 1 3 1 = 1 . 2 3 0 9 5 9 4 1 7 3 4 1
Now we use the follwing formula for finding areas of parametric curves:
A = 2 1 ∥ ∮ r ( t ) × d t d r d t ∥
This integral reduces to
A = 2 1 ∥ ∫ t 1 t 2 r ( t ) × d t d r d t ∥
The integrand is as follows
r ( t ) × d t d r = ( r c + v 1 cos t + v 2 sin t ) × ( − v 1 sin t + v 2 cos t )
Evaluating the cross product, results in
r ( t ) × d t d r = ( r c × v 1 ) ( − sin t ) + ( r c × v 2 ) ( cos t ) + ( v 1 × v 2 )
The cross products have only a z-component that is nonzero. So this will be the magnitude of the vector. In particular,
r c × v 1 = [ 0 , 0 , 3 ] T , r c × v 2 = [ 0 , 0 , − 3 ] , v 1 × v 2 = [ 0 , 0 , 9 ]
Therefore, the area is given by
A = 2 1 ∫ t 1 t 2 ( 3 ( − sin t ) − 3 cos t + 9 ) d t
A = 2 1 { 3 ( c o s ( t 2 ) − c o s ( t 1 ) ) − 3 ( s i n ( t 2 ) − s i n ( t 1 ) ) + 9 ( t 2 − t 1 ) }
Substituting the values of t 1 and t 2 , we obtain,
A = 2 . 1 8
Let P = ( − 1 , − 1 ) denote the center of the circle whose equation is ( x + 1 ) 2 + ( y + 1 ) 2 = 3 2 . Let Q and R be the intersection points between the circle with the y -axis and the x -axis, respectively.
We first find the coordinates of Q and R , respectively.
At point Q , x = 0 ⇒ ( 0 + 1 ) 2 + ( y + 1 ) 2 = 3 2 ⇒ y = 8 − 1 , we take the positive root only. Thus, Q = ( 0 , 8 − 1 ) .
Likewise, we get R = ( 8 − 1 , 0 ) .
The area of the orange region can be expressed as the sum of the area of the purple region and the area of the yellow region as shown in the figure on the right.
The area of the purple region represents the area of the right triangle O Q R ,
Area purple = 2 1 × base × height = 2 1 ( 8 − 1 ) 2 = 2 9 − 2 2 .
The area of the the yellow region represents the area of the segment Q P R , let θ = Q P R , then
Area yellow = 2 1 r 2 ( θ − sin θ ) = 2 9 ( θ − sin θ ) .
The acute angle θ can be calculated by applying the cosine rule on the triangle P Q R ,
cos θ = 2 ( P Q ) ( P R ) ( P Q ) 2 + ( P R ) 2 − ( Q R ) 2 = 2 ( 3 ) ( 3 ) ( 3 2 ) + ( 3 2 ) − ( ( 8 − 1 ) 2 + ( 8 − 1 ) 2 ) = 9 4 2 ⇒ sin θ = 1 − cos 2 θ = 9 7 .
Continue where we left off, we have Area yellow = 2 9 ( arccos ( 9 4 2 ) − 9 7 ) .
Thus, adding the two areas gives the desired answer
Area orange = = = ≈ Area purple + Area orange 2 9 − 2 2 + 2 9 ( arccos ( 9 4 2 ) − 9 7 ) 2 9 ( arccos ( 9 4 2 ) + 9 2 ) − 2 2 2 . 1 8