First think & then solve.
What number should replace the question mark ? 9 2 6 : 2 4 7 9 9 : 7 2 1 0 0 : 0 0 9 5 6 : ?
Check your IQ level through the test : IQ Test
The answer is 51.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Check your solution point 2 it should be 72.
Let your number be equal to x. Pick the smallest digit in 956 which is 5, which will be your last digit. then subtract 5 to the last digit of 956 ,6, which is equal to 1. There we have 51.
same as 926. pick 2, subtract 2 to 6, 4 there we have 24.
I thought way too outside the box for this one, but I removed the highest number in the group, took the remaining number and the subtracted it by the smaller of the 2. For example: 926. Remove the 9 leaving you with 26. 2 is the smaller number out of 2 and 6 so 26 - 2 = 24.
The algorithm is to multiply the hundreds digit by the tens digit, and then add the ones digit to the product. Hence,
1) (9*2) + 6 = 24
2) (7*9) + 9 = 72
3) (1*0) + 0 = 00
4) (9*5) + 6 = 51
First digit × second digit + third digit.
haha at first I thought 1) 6= 2+4 2) 9= 7+2 3) 0 = 0+ 0 4) 6= depend on us :) however, it seemed incomprehensive.
The Easiest Way to Solve Questions Like This is To Look for The Pattern. In this case, the pattern is multiplying the first two digits and adding the last digit to the product.
A trick to solving these questions, is to take a look and see that one of them has the answer of 00, so there must be some multiplying or stuff of the sort...
There are INFINITELY MANY ANSWERS to this problem
If I design a function like this:-
y = ( 9 2 6 − 7 9 9 ) × ( 9 2 6 − 1 0 0 ) × ( 9 2 6 − 9 5 6 ) 2 4 × ( x − 7 9 9 ) × ( x − 1 0 0 ) × ( x − 9 5 6 ) + ( 7 9 9 − 9 2 6 ) × ( 7 9 9 − 1 0 0 ) × ( 7 9 9 − 9 5 6 ) 7 2 × ( x − 9 2 6 ) × ( x − 1 0 0 ) × ( x − 9 5 6 ) + k × ( 9 5 6 − 9 2 6 ) × ( 9 5 6 − 7 9 9 ) × ( 9 5 6 − 1 0 0 ) ( x − 9 2 6 ) × ( x − 7 9 9 ) × ( x − 1 0 0 )
I can get any value k for x = 9 5 6 which is valid.
Since, by putting x = 9 2 6 , 7 9 9 , 1 0 0 , I'm getting the values you want i.e. 2 4 , 7 2 , 0 0 respectively.
I think the question is not valid. Maybe I thought too much. Calvin Lin Sandeep Bhardwaj
Remove the highest number, subtract the first digit of the remaining number to the remaining number.
926: remove 9, the remaining number is 26, subtract the first digit of the remaining number, 26-2 = 24
799: remove 9; 79 -7 = 72
100: remove 1; 00-0 = 00
956: remove 9; 56 - 5 = 51
Answer is 51.
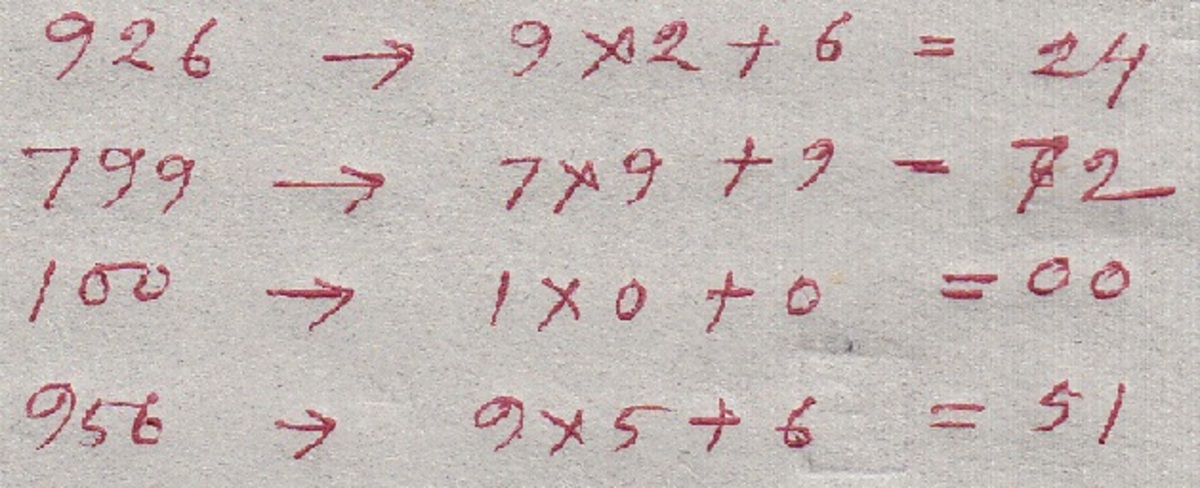
1) 9*2+6=24
2) 7*9+9=72
3)1*0+0=00
4)9*5+6 = 5 1