Fishy Information

Geometry Level 5

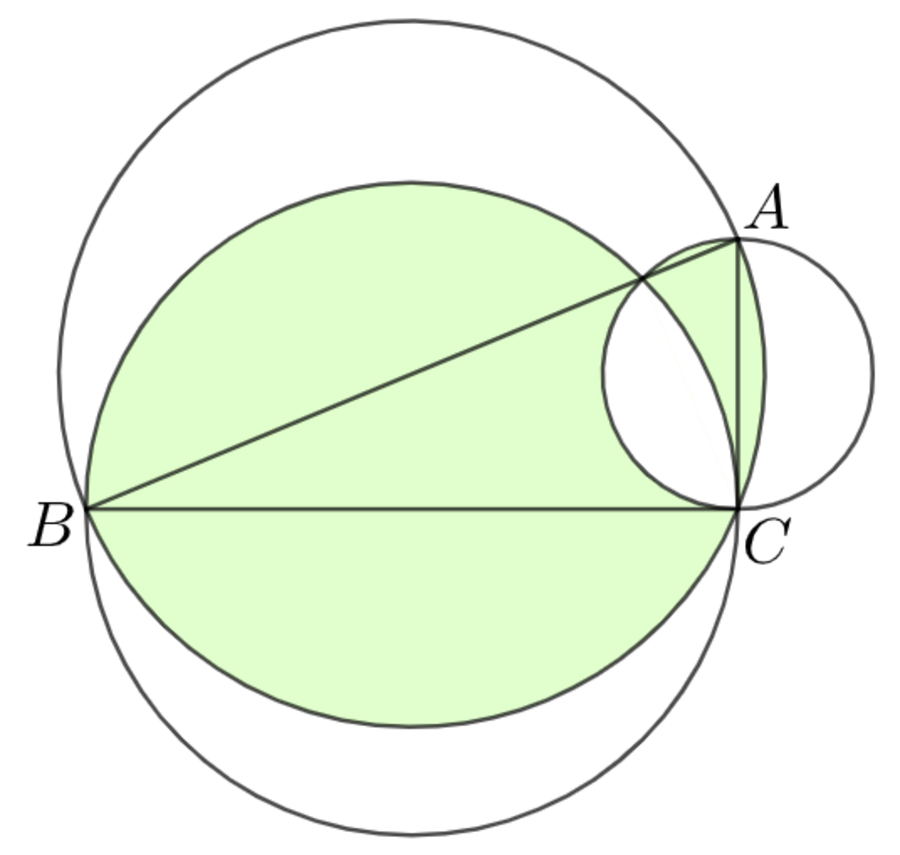
The three circles overlap each other, such that points A , B , C A,B,C are their intersection points as shown above. It is known that triangle A B C ABC has side lengths ∣ B C ‾ ∣ = 1 + 2 |\overline{BC}| = 1 + \sqrt{2} and ∣ A C ‾ ∣ = 1 |\overline{AC}| = 1 . In addition, all its sides represent the respective diameters of the circles.

If the area sum of the green region can be expressed as

A B ( C + D E ) π \dfrac{A}{B}\left(C + D\sqrt{E} \right) \pi

where A , B , C , D , E A,B,C,D,E are positive integers, gcd ⁡ ( A , B ) = gcd ⁡ ( C , D ) = 1 \gcd (A,B) = \gcd (C,D) = 1 and E E is square-free, input A + B + C + D + E A + B + C + D + E as your answer.


The answer is 19.

Michael Huang by Michael Huang , 29, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

David Vreken
Feb 17, 2021

Let D D , E E , and F F be the centers of each circle, and let G G be the other intersection point of circles:

Since A B AB , A C AC , and B C BC are diameters, by Thales's Theorem ∠ A C B = ∠ A G C = ∠ B G C = 90 ° \angle ACB = \angle AGC= \angle BGC = 90° , which means △ A B C ∼ △ A C G ∼ △ C B G \triangle ABC \sim \triangle ACG \sim \triangle CBG by AA similarity.

The area of △ A B C \triangle ABC is A △ A B C = 1 2 ⋅ B C ⋅ A C = 1 2 ⋅ ( 1 + 2 ) ⋅ 1 = 1 + 2 2 A_{\triangle ABC} = \cfrac{1}{2} \cdot BC \cdot AC = \cfrac{1}{2} \cdot (1 + \sqrt{2}) \cdot 1 = \cfrac{1 + \sqrt{2}}{2} .

By the Pythagorean Theorem on △ A B C \triangle ABC , A B = A C 2 + B C 2 = ( 1 + 2 ) 2 + 1 2 = 4 + 2 2 AB = \sqrt{AC^2 + BC^2} = \sqrt{(1 + \sqrt{2})^2 + 1^2} = \sqrt{4 + 2\sqrt{2}} .

Also from △ A B C \triangle ABC , ∠ A B C = tan ⁡ − 1 A C B C = tan ⁡ − 1 1 1 + 2 = 22.5 ° \angle ABC = \tan^{-1} \cfrac{AC}{BC} = \tan^{-1} \cfrac{1}{1 + \sqrt{2}} = 22.5° , and its central angle ∠ A F C = 2 ⋅ 22.5 ° = 45 ° \angle AFC = 2 \cdot 22.5° = 45° .

By similar triangles, ∠ A B C = ∠ A C G = ∠ C B G = 22.5 ° \angle ABC = \angle ACG = \angle CBG = 22.5° , so central angles ∠ A E G = ∠ C D G = 45 ° \angle AEG = \angle CDG = 45° .

Let the A G C 1 A_{GC1} be the area between G C GC and the arc G C GC (on the right side). As a difference between sector C D G CDG and △ C D G \triangle CDG ,

A G C 1 = ∠ C D G 360 ° ⋅ π ⋅ C D 2 − 1 2 ⋅ C D 2 ⋅ sin ⁡ ∠ C D G = 45 ° 360 ° ⋅ π ⋅ ( 1 + 2 2 ) 2 − 1 2 ⋅ ( 1 + 2 2 ) 2 ⋅ sin ⁡ 45 ° = ( 1 8 π − 2 4 ) ( 3 + 2 2 4 ) A_{GC1} = \cfrac{\angle CDG}{360°} \cdot \pi \cdot CD^2 - \cfrac{1}{2} \cdot CD^2 \cdot \sin \angle CDG = \cfrac{45°}{360°} \cdot \pi \cdot \bigg(\cfrac{1 + \sqrt{2}}{2} \bigg)^2 - \cfrac{1}{2} \cdot \bigg(\cfrac{1 + \sqrt{2}}{2} \bigg)^2 \cdot \sin 45° = \bigg(\cfrac{1}{8}\pi - \cfrac{\sqrt{2}}{4}\bigg)\bigg(\cfrac{3 + 2\sqrt{2}}{4} \bigg)

Similarly,

A B G = ∠ B D G 360 ° ⋅ π ⋅ B D 2 − 1 2 ⋅ B D 2 ⋅ sin ⁡ ∠ B D G = 135 ° 360 ° ⋅ π ⋅ ( 1 + 2 2 ) 2 − 1 2 ⋅ ( 1 + 2 2 ) 2 ⋅ sin ⁡ 135 ° = ( 3 8 π − 2 4 ) ( 3 + 2 2 4 ) A_{BG} = \cfrac{\angle BDG}{360°} \cdot \pi \cdot BD^2 - \cfrac{1}{2} \cdot BD^2 \cdot \sin \angle BDG = \cfrac{135°}{360°} \cdot \pi \cdot \bigg(\cfrac{1 + \sqrt{2}}{2} \bigg)^2 - \cfrac{1}{2} \cdot \bigg(\cfrac{1 + \sqrt{2}}{2} \bigg)^2 \cdot \sin 135° = \bigg(\cfrac{3}{8}\pi - \cfrac{\sqrt{2}}{4}\bigg)\bigg(\cfrac{3 + 2\sqrt{2}}{4} \bigg)

A A G = ∠ A E G 360 ° ⋅ π ⋅ A E 2 − 1 2 ⋅ A E 2 ⋅ sin ⁡ ∠ A E G = 45 ° 360 ° ⋅ π ⋅ ( 1 2 ) 2 − 1 2 ⋅ ( 1 2 ) 2 ⋅ sin ⁡ 45 ° = ( 1 8 π − 2 4 ) ( 1 4 ) A_{AG} = \cfrac{\angle AEG}{360°} \cdot \pi \cdot AE^2 - \cfrac{1}{2} \cdot AE^2 \cdot \sin \angle AEG = \cfrac{45°}{360°} \cdot \pi \cdot \bigg(\cfrac{1}{2} \bigg)^2 - \cfrac{1}{2} \cdot \bigg(\cfrac{1}{2} \bigg)^2 \cdot \sin 45° = \bigg(\cfrac{1}{8}\pi - \cfrac{\sqrt{2}}{4}\bigg)\bigg(\cfrac{1}{4} \bigg)

A G C 2 = ∠ C E G 360 ° ⋅ π ⋅ E C 2 − 1 2 ⋅ E C 2 ⋅ sin ⁡ ∠ C E G = 135 ° 360 ° ⋅ π ⋅ ( 1 2 ) 2 − 1 2 ⋅ ( 1 2 ) 2 ⋅ sin ⁡ 135 ° = ( 3 8 π − 2 4 ) ( 1 4 ) A_{GC2} = \cfrac{\angle CEG}{360°} \cdot \pi \cdot EC^2 - \cfrac{1}{2} \cdot EC^2 \cdot \sin \angle CEG = \cfrac{135°}{360°} \cdot \pi \cdot \bigg(\cfrac{1}{2} \bigg)^2 - \cfrac{1}{2} \cdot \bigg(\cfrac{1}{2} \bigg)^2 \cdot \sin 135° = \bigg(\cfrac{3}{8}\pi - \cfrac{\sqrt{2}}{4}\bigg)\bigg(\cfrac{1}{4} \bigg)

A A C = ∠ A F C 360 ° ⋅ π ⋅ A F 2 − 1 2 ⋅ A F 2 ⋅ sin ⁡ ∠ A F C = 45 ° 360 ° ⋅ π ⋅ ( 4 + 2 2 2 ) 2 − 1 2 ⋅ ( 4 + 2 2 2 ) 2 ⋅ sin ⁡ 45 ° = ( 1 8 π − 2 4 ) ( 4 + 2 2 4 ) A_{AC} = \cfrac{\angle AFC}{360°} \cdot \pi \cdot AF^2 - \cfrac{1}{2} \cdot AF^2 \cdot \sin \angle AFC = \cfrac{45°}{360°} \cdot \pi \cdot \bigg(\cfrac{\sqrt{4 + 2\sqrt{2}}}{2} \bigg)^2 - \cfrac{1}{2} \cdot \bigg(\cfrac{\sqrt{4 + 2\sqrt{2}}}{2} \bigg)^2 \cdot \sin 45° = \bigg(\cfrac{1}{8}\pi - \cfrac{\sqrt{2}}{4}\bigg)\bigg(\cfrac{4 + 2\sqrt{2}}{4} \bigg)

A B C = ∠ B F C 360 ° ⋅ π ⋅ B F 2 − 1 2 ⋅ B F 2 ⋅ sin ⁡ ∠ B F C = 135 ° 360 ° ⋅ π ⋅ ( 4 + 2 2 2 ) 2 − 1 2 ⋅ ( 4 + 2 2 2 ) 2 ⋅ sin ⁡ 135 ° = ( 3 8 π − 2 4 ) ( 4 + 2 2 4 ) A_{BC} = \cfrac{\angle BFC}{360°} \cdot \pi \cdot BF^2 - \cfrac{1}{2} \cdot BF^2 \cdot \sin \angle BFC = \cfrac{135°}{360°} \cdot \pi \cdot \bigg(\cfrac{\sqrt{4 + 2\sqrt{2}}}{2} \bigg)^2 - \cfrac{1}{2} \cdot \bigg(\cfrac{\sqrt{4 + 2\sqrt{2}}}{2} \bigg)^2 \cdot \sin 135° = \bigg(\cfrac{3}{8}\pi - \cfrac{\sqrt{2}}{4}\bigg)\bigg(\cfrac{4 + 2\sqrt{2}}{4} \bigg)

The area of the green region is then A green = A △ A B C − A G C 1 − A G C 2 + A B G + A A G + A A C + A B C = 1 8 ( 5 + 3 2 ) π A_{\text{green}} = A_{\triangle ABC} - A_{GC1} - A_{GC2} + A_{BG} + A_{AG} + A_{AC} + A_{BC} = \cfrac{1}{8}(5 + 3\sqrt{2})\pi .

Therefore, A = 1 A = 1 , B = 8 B = 8 , C = 5 C = 5 , D = 3 D = 3 , E = 2 E = 2 , and A + B + C + D + E = 19 A + B + C + D + E = \boxed{19} .

3 Helpful 3 Interesting 4 Brilliant 0 Confused

I wonder if there's a faster and less obvious way of solving this. I did it the same as you did, @David Vreken . P.S. For the record A , B , C , D A, B, C, D and E E are the first 5 5 different Fibonacci numbers. What a coincidence...or is it?

Veselin Dimov - 3 months, 2 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...