Fit in the Hexagon!

Geometry Level 3

Given below, the red curves represent the curves,

y = e − x 2 y = e^{-x^2} and

y = − e − x 2 y = -e^{-x^2}

Find the area of the green regular hexagon.


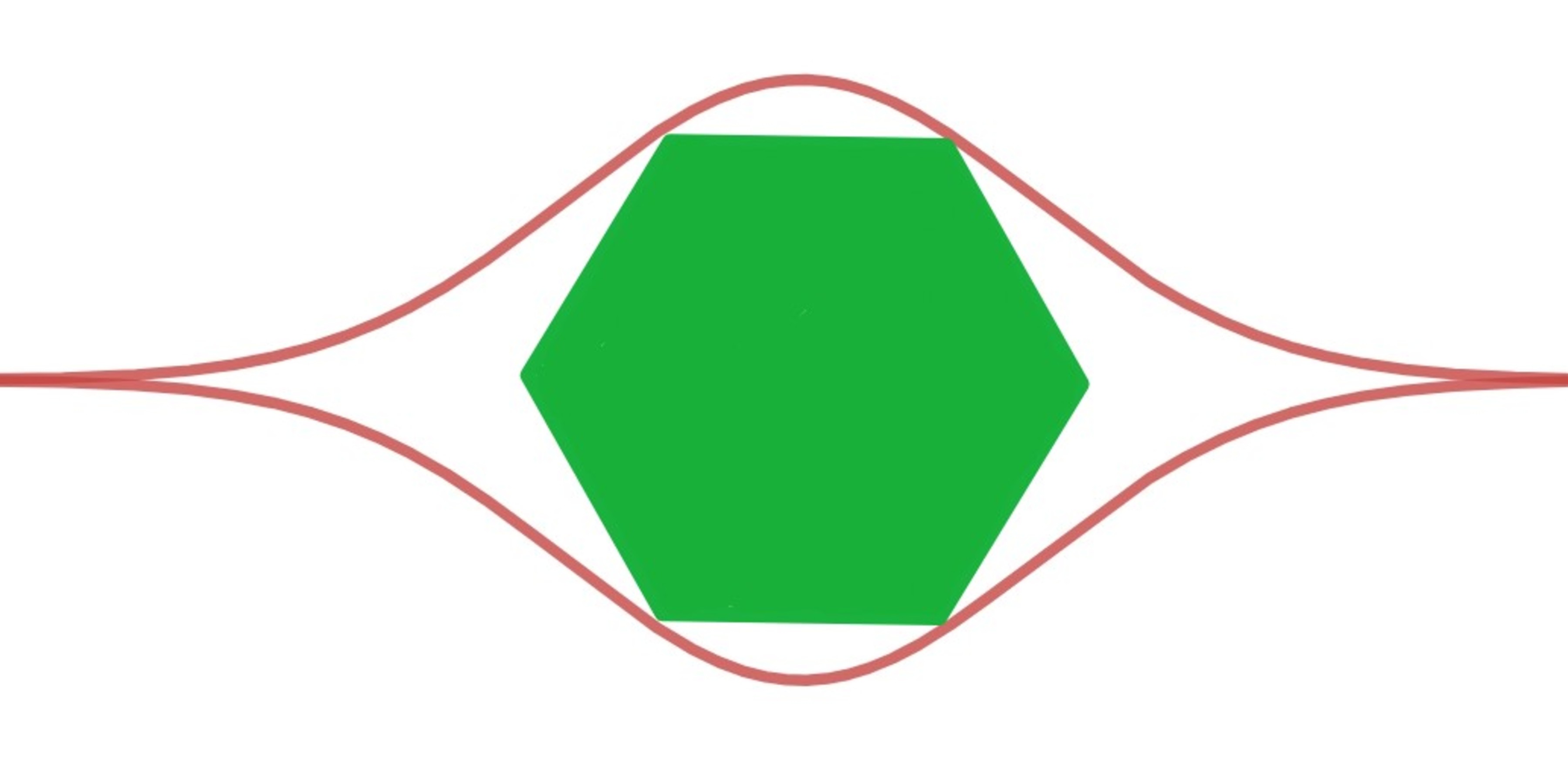
The answer is 2.24957286644.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Jeremy Galvagni
Nov 21, 2018

Find the intersection of the curve y = e − x 2 y=e^{-x^{2}} and the line y = 3 x y=\sqrt{3}x using numerical means. x ≈ 0.4650606173 x\approx 0.4650606173

The side length of the hexagon is 2 x 2x and the area of the hexagon is 3 3 2 ( 2 x ) 2 ≈ 2.24766201 \frac{3\sqrt{3}}{2}(2x)^{2} \approx \boxed{2.24766201}

(I believe my solution is more accurate than the official one.)

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Yeah I approximated x = 0.4651 x = 0.4651 so I got a slightly deviated answer. Thanks for your solution.

A Former Brilliant Member - 2 years, 6 months ago

Incidentally, a circle which will fit exactly inside this "Gaussian Eye" will have a radius of 0.9200 and an area of 2.659

It will have the equation: x^2 + y^2 = (0.9200978)^2

A bit larger than that Hexagon you have in the figure above.

Vijay Simha - 2 years, 6 months ago

Log in to reply

The original question was infact about the max area of a Circle within the curves, I didn't create this, I chenged Circle to Hexagon.

A Former Brilliant Member - 2 years, 6 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...