Fitting a parabola to four Cartesian points

Geometry Level 3

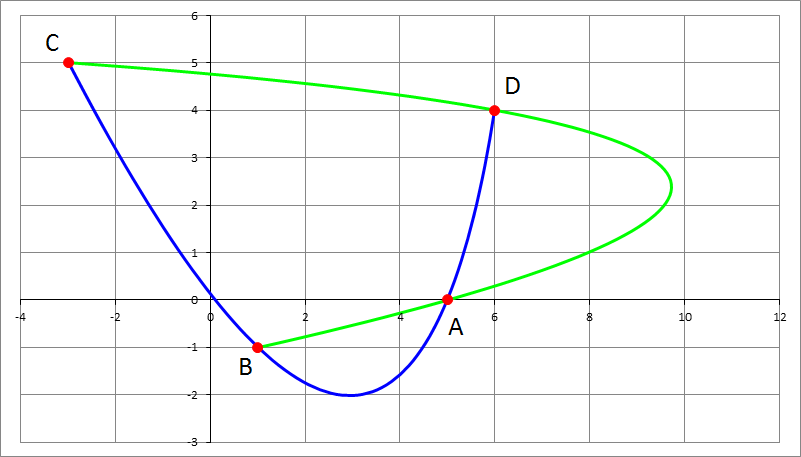
In the Cartesian $xy$ -plane, you are given the following four points, $A (5, 0), B(1, -1), C(-3, 5) , D(6, 4)$ . You want to fit a parabola that will pass through the four points. As it turns out, there are two such parabolas shown in the figure below in blue and green colors. Each of them can be represented by the parametric equation:

$r = r_v + R(\theta) r'$

where $r = (x(t), y(t) )$ , $r_v = ( r_{vx}, r_{vy})$ is the vertex of the parabola, $r' = ( t, at^2 )$ , with $a \gt 0$ , and

$R = \begin{bmatrix} \cos \theta && -\sin \theta \\ \sin \theta && \cos \theta \end{bmatrix}$

where $\theta \in [0, 2 \pi)$ is in radians. Find the two fitting parabolas to the four given points, and find $S$ where,

$S = \displaystyle \sum_{i= 1}^{2} r_{vx_i} + r_{vy_i} + a_i + \theta_i$

where index $i$ indicates the $i$ -th parabola. Enter the value of $\lfloor 10^4 S \rfloor$ as your answer. The figure is drawn to scale.

The answer is 166436.

1 solution

Steven Chase
Apr 1, 2019

The unknowns are $(r_{vx}, r_{vy}, \theta, a, t_A, t_B, t_C, t_D)$ . We can solve the following eight non-linear equations for the eight unknowns:

$A_x = r_{vx} + cos \theta \, t_A - sin \theta \, a \, t_A^2 \\ A_y = r_{vy} + sin \theta \, t_A + cos \theta \, a \, t_A^2 \\ B_x = r_{vx} + cos \theta \, t_B - sin \theta \, a \, t_B^2 \\ B_y = r_{vy} + sin \theta \, t_B + cos \theta \, a \, t_B^2 \\ C_x = r_{vx} + cos \theta \, t_C - sin \theta \, a \, t_C^2 \\ C_y = r_{vy} + sin \theta \, t_C + cos \theta \, a \, t_C^2 \\ D_x = r_{vx} + cos \theta \, t_D - sin \theta \, a \, t_D^2 \\ D_y = r_{vy} + sin \theta \, t_D + cos \theta \, a \, t_D^2$

Solving using multivariate Newton-Raphson yields the one parabola:

$r_{vx} = 3.216840 \\ r_{vy} = -1.994092 \\ \theta = 0.192811\\ a = 0.355328$

And the other:

$r_{vx} = 9.731134 \\ r_{vy} = 2.412849 \\ \theta = 1.633877 \\ a = 1.094929$

Fitting a parabola to four Cartesian points

The answer is 166436.

1 solution

0 pending reports