Fitting a rectangular hyperbola to a rectangle

Geometry Level 4

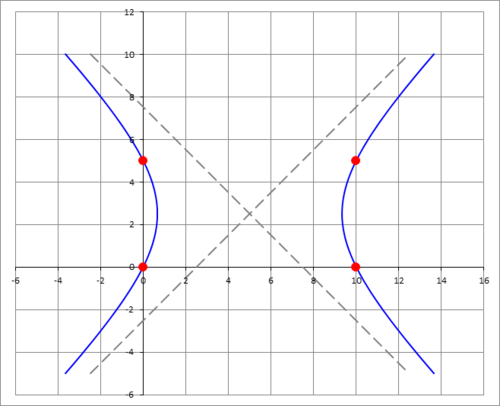
The four vertices of a rectangle are given by: $A(0, 0), B(10, 0), C(10, 5), D(0, 5)$ . We want to fit a rectangular hyperbola to these four points. A rectangular hyperbola is one having equal semi-axes, and is characterized by its asymptotes crossing at right angles. Find the common semi-axis of this hyperbola. The semi-axis can be expressed as $\dfrac{a \sqrt{b} }{c}$ for positive integers $a, b, c$ , where $a, b$ are coprime, and $c$ square-free. Enter $a + b + c$ .

The answer is 10.

1 solution

Tom Engelsman
Apr 17, 2021

The center of the required hyperbola must coincide with the centroid of the given rectangular region, namely $(x,y) = (5, 5/2).$ This gives us the equation of the hyperbola:

$\Large \frac{(x-5)^2}{a^2} - \frac{(y-5/2)^2}{b^2} = 1$

Since this hyperbola is rectangular, we conclude $a = b$ which results in $(x-5)^2 - (y-5/2)^2 = a^2$ . If we then substitute any one of the rectangular region's vertices into our hyperbola equation (WLOG use $(0,0)$ ), we obtain:

$(0-5)^2 - (0-5/2)^2 = 25 - 25/4 = 25(\frac{3}{4}) = a^2 \Rightarrow \boxed{a = \frac{5\sqrt{3}}{2}}.$

or $5+3+2 = \boxed{10}.$

Fitting a rectangular hyperbola to a rectangle

The answer is 10.

1 solution

0 pending reports