Fitting a Square to Four Points

Geometry Level 3

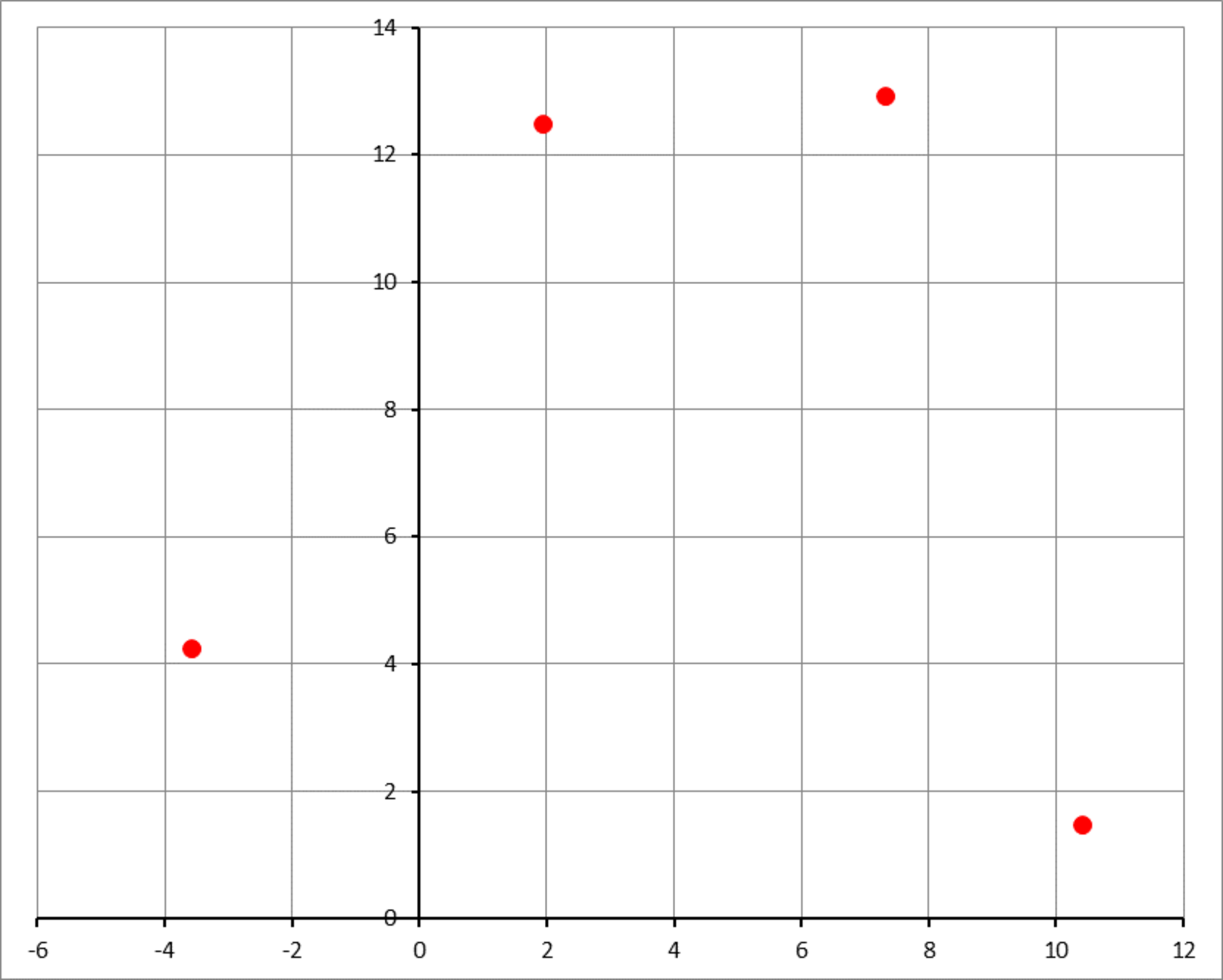
As the figure above shows, we are given the following 4 points in the XY plane, listed in counter-clockwise direction:

$P_1 = (1.956292884, 12.45603043)$

$P_2 = (-3.541888022, 4.227012093)$

$P_3 = (10.44287164, 1.437742959)$

$P_4 = (7.341227934, 12.90173469)$

We want to fit a square of general orientation to these four points. The only thing known about the points is that each point lies on a different side. They are ordered counter-clockwise to correspond with the sides.

Find the center $(x_0, y_0)$ and the side length $a$ of the fitting square, submit as your answer the concatenation of $\big[ 100 x_0 \big]$ and $\big[ 100 y_0 \big]$ and $\big[ 100 a \big]$ . For example, if the center is $(2.379, 5.6178)$ and the side length is $12.9315$ , then your answer should be $2385621293$ .

Inspiration

The answer is 4135461390.

1 solution

Hosam Hajjir
Dec 26, 2017

Following the solution of Mark Hennings for the original problem posted by Steven Chase, we define the direction vectors of the sides of the square as

$u = (\cos \theta , \sin \theta)$ and $v = (-\sin \theta, \cos \theta)$

It then follows by projecting the vector $(P_4 - P_2)$ onto $u$ and $(P1 - P3)$ onto $v$ , both projections being equal to the side length $a$ , namely,

$(P_4 - P_2) \cdot u = (P_1 - P_3) \cdot v = a$

which results in $\theta = 0.623$ (radians). Next, we can find the side length from the above equation also by plugging in the value of $\theta$ found. The value thus found is $a = 13.90$ .

What is left to find the center, and for that we can write two equations in the two unknown coordinates of the center $r_C$ , namely,

$(P_1 - r_C) \cdot v = \dfrac{1}{2} a$

and

$(P_2 - r_C) \cdot u = - \dfrac{1}{2} a$

Solving this linear system gives $r_C = (4.13, 5.46)$

Therefore, the answer is $4135461390$

Below is the fitted square.

Fitting a Square to Four Points

The answer is 4135461390.

1 solution

0 pending reports