Fitting an ellipse to four points
You are given four points: A ( 6 , 2 ) , B ( 4 , 3 ) , C ( − 1 , 1 ) , D ( 1 , − 2 ) . You want to fit an ellipse in standard orientation to these four points. The equation of this ellipse is:
a 2 ( x − x 0 ) 2 + b 2 ( y − y 0 ) 2 = 1
Identify the ellipse, and enter the sum a + b + x 0 + y 0 .
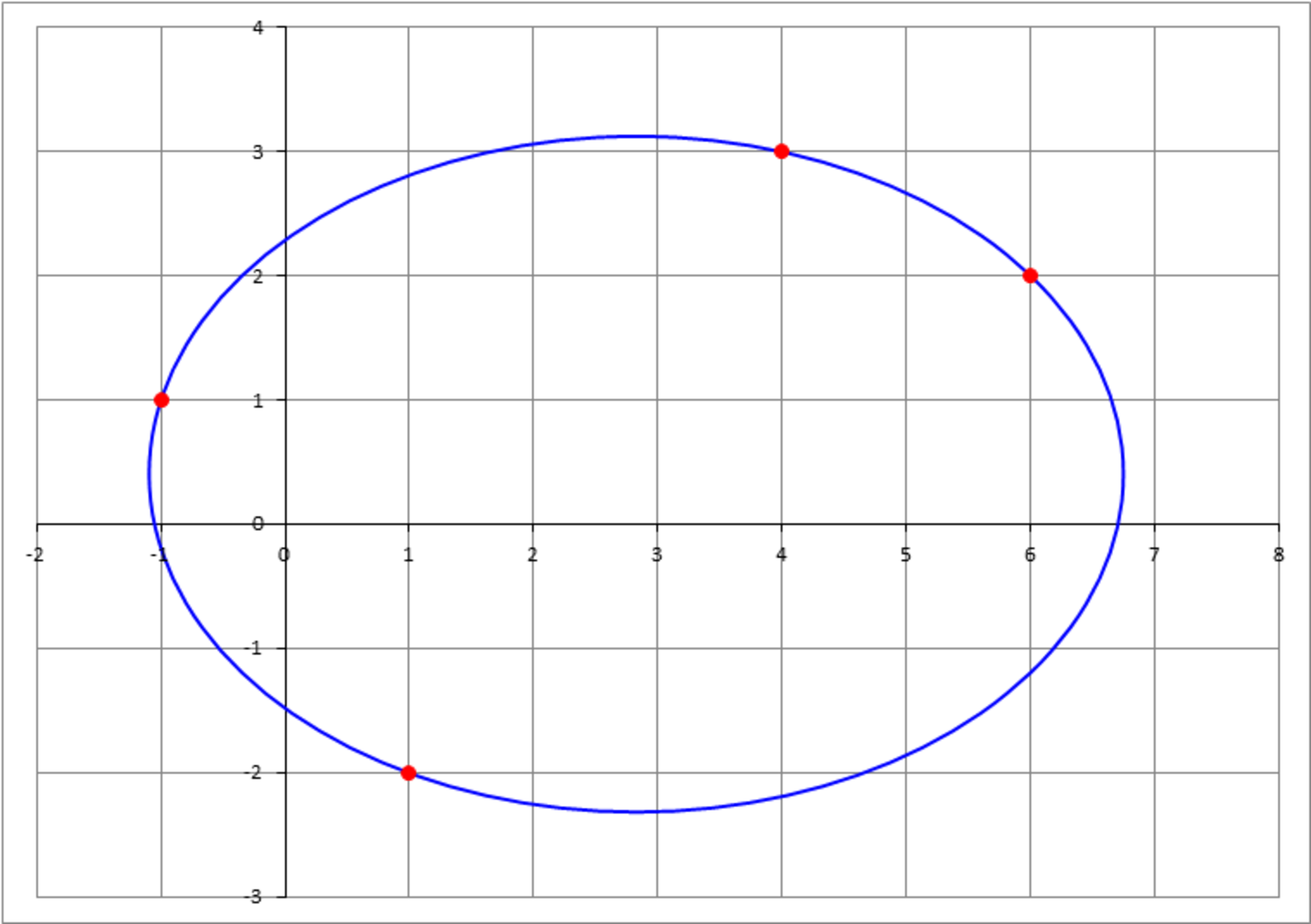
The answer is 9.869.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Using the given informations we get two sets of values of ( X C , Y C , a , b ) , namely ( 3 . 5 , 0 , 3 . 3 2 4 , 3 . 0 3 4 ) and ( 2 . 8 2 , 0 . 4 1 , 3 . 9 2 , 2 . 7 2 ) . In the first case, the required sum is 9 . 8 5 9 and in the second case it is 9 . 8 6 8 .
Can you explain how you got these numbers in more detail ? Because I didn't get two sets of values, only one set.
Wolframalpha