Fitting an Equilateral Triangle Through 3 Points
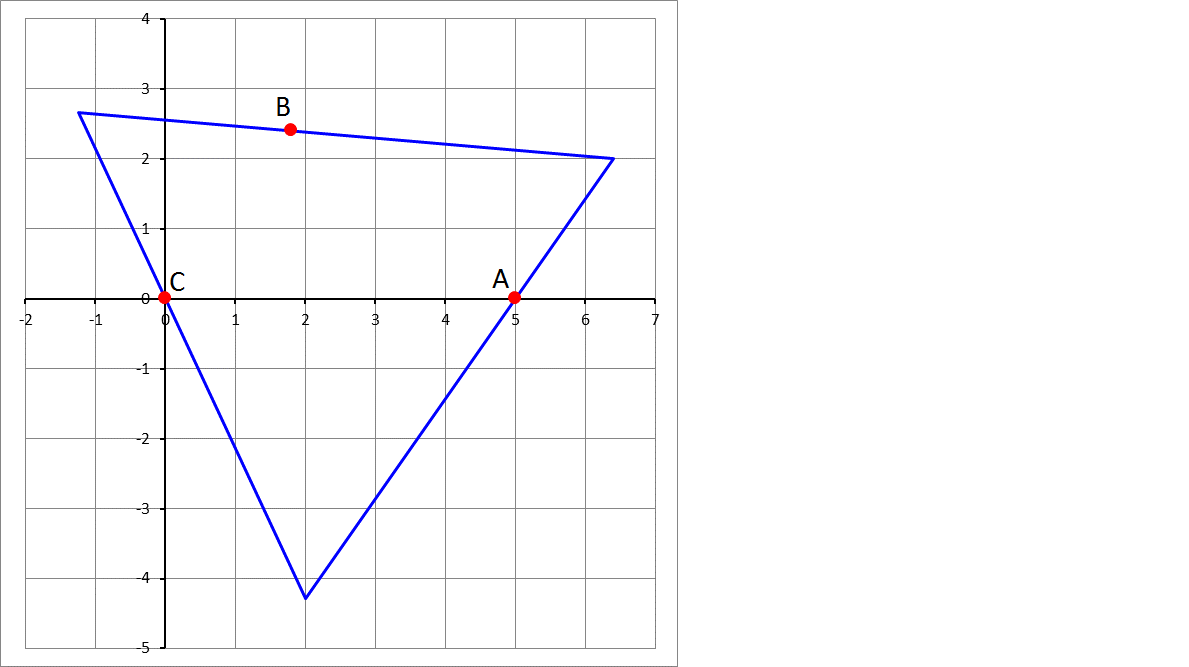
Given three points in the Cartesian plane, A ( 5 , 0 ) , B ( 1 . 8 , 2 . 4 ) , and C ( 0 , 0 ) , you want to find an equilateral triangle whose sides pass through points A , B , and C . In addition, it is required that the side passing through point A make an angle of + 4 5 ∘ with the positive x -axis direction. Find the side length of this equilateral triangle rounded to 5 decimal places. Figure above not drawn to scale
The answer is 7.29728.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
With a little bit calculation, we know that A B = 4 , B C = 3 , A C = 5 also A C will form an angle 4 5 ∘ with a side of the equilateral triangle. Construct an ex-triangle with vertices D , E , F (see the figure below)
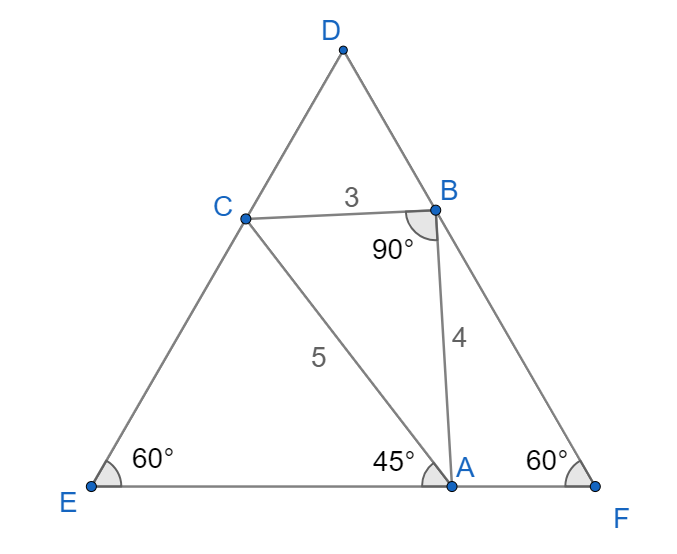
sin 4 5 ∘ E C = sin 6 0 ∘ 5 gets E C = 3 5 6 ;
E A = E C cos 6 0 ∘ + 5 cos 4 5 ∘ = 6 1 5 2 + 5 6 .
Assume the angles ∠ B A C = θ , ∠ B A F = α , we then have tan θ = 4 3 and tan ( θ + α ) = tan 1 3 5 ∘ = − 1 , so
tan α = tan ( θ + α − θ ) = 1 + tan ( θ + α ) tan α tan ( θ + α ) − tan θ = 1 − 4 3 − 1 − 4 3 = − 7
So other trigonometric of α will be sin α = 5 2 7 and cos α = − 5 2 1 .
Finding B F :
sin α B F = sin 6 0 ∘ 4 to get B F = 1 5 2 8 6 , then we find A F by using same method:
A F = 4 cos α + B F cos 6 0 ∘ = 3 0 − 1 2 2 + 2 8 6 .
Adding up E A and A F will give us the side length of the equilateral triangle:
E F = E A + A F = 6 1 5 2 + 5 6 + 3 0 − 1 2 2 + 2 8 6 = 3 0 6 3 2 + 5 3 6
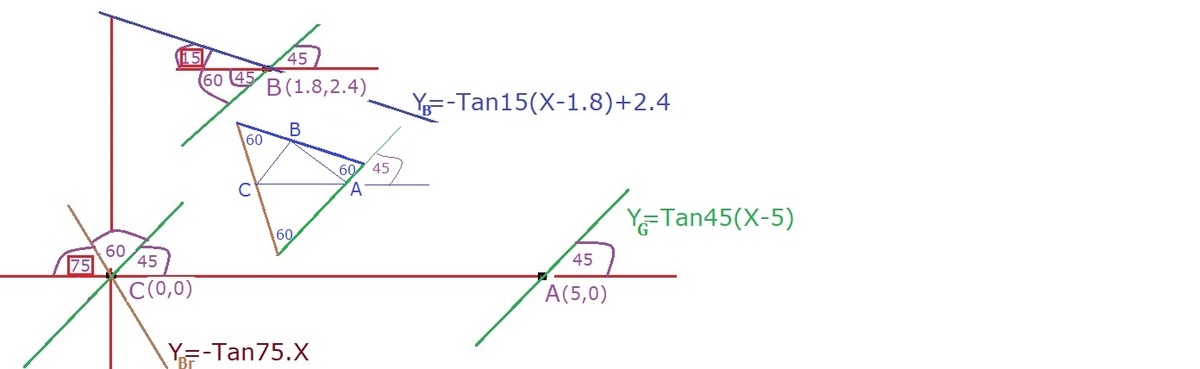 A
s
s
e
e
n
f
r
o
m
t
h
e
s
k
e
t
c
h
,
t
h
e
Y
G
,
Y
B
,
Y
B
r
t
h
e
e
q
u
a
t
i
o
n
s
o
f
t
h
e
Δ
s
i
d
e
s
a
r
e
:
−
Y
G
=
X
−
5
.
Y
B
=
−
T
a
n
1
5
(
X
−
1
.
8
)
+
2
.
4
.
Y
B
r
=
−
T
a
n
7
5
.
X
∴
Y
G
a
n
d
Y
B
i
n
t
e
r
s
e
c
t
a
t
v
e
r
t
e
x
(
X
G
−
B
,
Y
G
−
B
)
=
(
1
+
T
a
n
1
5
7
.
4
+
1
.
8
T
a
n
1
5
,
1
+
T
a
n
1
5
7
.
4
+
1
.
8
T
a
n
1
5
−
5
)
A
n
d
Y
G
a
n
d
Y
B
r
i
n
t
e
r
s
e
c
t
a
t
v
e
r
t
e
x
(
X
G
−
B
r
,
Y
G
−
B
r
)
=
(
1
+
T
a
n
7
5
5
,
1
+
T
a
n
7
5
5
−
5
)
∴
t
h
e
s
i
d
e
l
e
n
g
t
h
=
(
1
+
T
a
n
1
5
7
.
4
+
1
.
8
T
a
n
1
5
−
1
+
T
a
n
7
5
5
)
2
,
(
1
+
T
a
n
1
5
7
.
4
+
1
.
8
T
a
n
1
5
−
5
−
1
+
T
a
n
7
5
5
+
5
)
2
=
2
∗
(
1
+
T
a
n
1
5
7
.
4
+
1
.
8
T
a
n
1
5
−
1
+
T
a
n
7
5
5
)
=
1
+
T
a
n
1
5
2
∗
(
7
.
4
−
3
.
2
T
a
n
1
5
)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
S
i
n
c
e
T
a
n
7
5
=
T
a
n
1
5
1
=
7
.
2
9
7
2
8
A
s
s
e
e
n
f
r
o
m
t
h
e
s
k
e
t
c
h
,
t
h
e
Y
G
,
Y
B
,
Y
B
r
t
h
e
e
q
u
a
t
i
o
n
s
o
f
t
h
e
Δ
s
i
d
e
s
a
r
e
:
−
Y
G
=
X
−
5
.
Y
B
=
−
T
a
n
1
5
(
X
−
1
.
8
)
+
2
.
4
.
Y
B
r
=
−
T
a
n
7
5
.
X
∴
Y
G
a
n
d
Y
B
i
n
t
e
r
s
e
c
t
a
t
v
e
r
t
e
x
(
X
G
−
B
,
Y
G
−
B
)
=
(
1
+
T
a
n
1
5
7
.
4
+
1
.
8
T
a
n
1
5
,
1
+
T
a
n
1
5
7
.
4
+
1
.
8
T
a
n
1
5
−
5
)
A
n
d
Y
G
a
n
d
Y
B
r
i
n
t
e
r
s
e
c
t
a
t
v
e
r
t
e
x
(
X
G
−
B
r
,
Y
G
−
B
r
)
=
(
1
+
T
a
n
7
5
5
,
1
+
T
a
n
7
5
5
−
5
)
∴
t
h
e
s
i
d
e
l
e
n
g
t
h
=
(
1
+
T
a
n
1
5
7
.
4
+
1
.
8
T
a
n
1
5
−
1
+
T
a
n
7
5
5
)
2
,
(
1
+
T
a
n
1
5
7
.
4
+
1
.
8
T
a
n
1
5
−
5
−
1
+
T
a
n
7
5
5
+
5
)
2
=
2
∗
(
1
+
T
a
n
1
5
7
.
4
+
1
.
8
T
a
n
1
5
−
1
+
T
a
n
7
5
5
)
=
1
+
T
a
n
1
5
2
∗
(
7
.
4
−
3
.
2
T
a
n
1
5
)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
S
i
n
c
e
T
a
n
7
5
=
T
a
n
1
5
1
=
7
.
2
9
7
2
8
The slope of the line passing through A is m A = tan − 1 4 5 ° = 1 . Since an equilateral triangle has 60° angles, the slope m B through B must satisfy the equation tan ( − 6 0 ° ) = 1 + m B m B − 1 , which solves to m B = − 2 + 3 , and the slope m C through C must satisfy the equation tan 6 0 ° = 1 + m C m C − 1 , which solves to m C = − 2 − 3 .
The equation of the line through A ( 5 , 0 ) with a slope of m A = 1 is y = x − 5 . The equation of the line through B ( 1 . 8 , 2 . 4 ) with a slope of m B = − 2 + 3 is y = ( − 2 + 3 ) x + 5 3 0 − 9 3 . And the equation of the line through C ( 0 , 0 ) with a slope of m C = − 2 − 3 is y = ( − 2 − 3 ) x .
The intersection of y = x − 5 and y = ( − 2 + 3 ) x + 5 3 0 − 9 3 is ( 1 5 6 9 + 1 4 3 , 1 5 − 6 + 1 4 3 ) , and the intersection of y = x − 5 and y = ( − 2 − 3 ) x is ( 6 1 5 − 5 3 , 6 − 1 5 − 5 3 ) , and the distance between these two points (and also the side length of the equilateral triangle) is 3 0 6 3 2 + 5 3 6 ≈ 7 . 2 9 7 2 8 .