Fitting an equilateral triangle to three points 2
Three points in the Cartesian plane are given by: A ( 1 , 1 ) , B ( 5 , 4 ) , C ( 3 , 7 ) . We want to draw an equilateral triangle of side length L that will pass through A , B and C , with one point on each side.
Find L m a x .
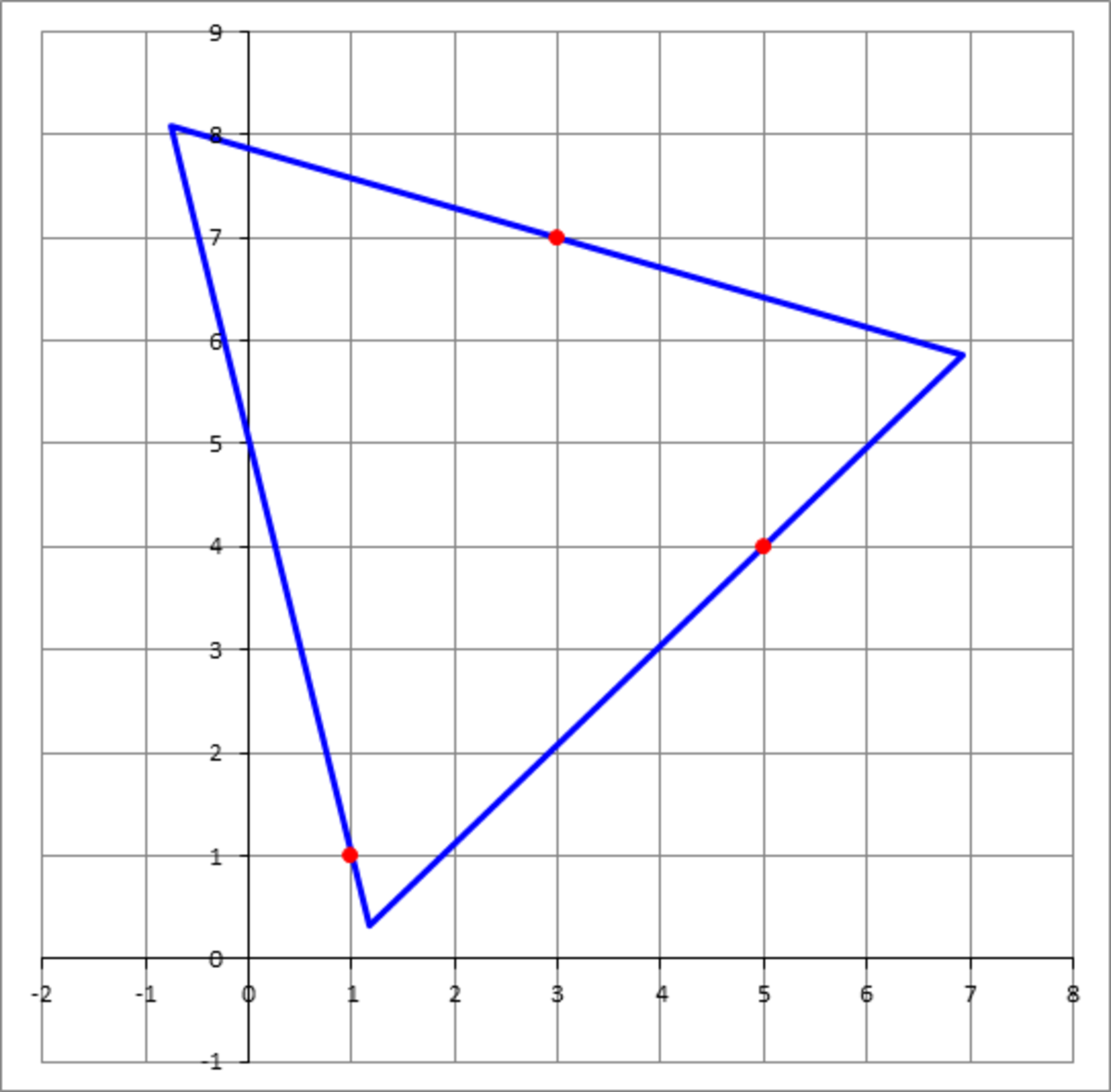
The answer is 9.673.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
If the fitted triangle is centered at r 0 and tilted by an angle θ from the standard orientation, then using simple geometry on the equilateral triangle, we can write the following equation iterated for the three points.
( P i − r 0 ) T R ( θ ) v i = 2 3 1 L , i = 1 , 2 , 3
where { P i } are the three given points, and R ( θ ) is the standard 2D rotation matrix, and is given by
R ( θ ) = [ cos θ sin θ − sin θ cos θ ]
And the { v i } are three unit vectors pointing from the center of the equilateral in standard orientation (without rotation) to the center of the three sides of the triangle, and they are given by,
v 1 = [ cos 6 π , sin 6 π ] T
v 2 = [ cos 6 5 π , sin 6 5 π ] T
v 3 = [ cos 2 3 π , sin 2 3 π ] T
Now the key trick here is to eliminate r 0 from the three equations, by simply adding them up. This is possible because v 1 + v 2 + v 3 = 0 .
Hence, the result of addition is a single equation,
P 1 T R ( θ ) v 1 + P 2 T R ( θ ) v 2 + P 3 T R ( θ ) v 3 = 2 3 L
The left hand side of the above equation is the sum of three quadratic forms, and can be expressed as a certain linear combination of cos θ and sin θ , so that the equation becomes,
A cos θ + B sin θ = C
where
A = i = 1 ∑ 3 P i x v i x + P i y v i y
B = i = 1 ∑ 3 P i y v i x − P i x v i y
C = 2 3 L
Now, this trigonometric equation has a solution only if the right side satisfies the following inequality,
− A 2 + B 2 ≤ C ≤ A 2 + B 2
And since A and B are known, we can compute the maximum of C and hence the maximum of L .
I want to delete this problem.
Don't delete the problem. Keep it as it is.
Let the vertices of the equilateral triangle be D , E , F , the point with position coordinates ( 1 , 1 ) be A , ( 5 , 4 ) be B , and ( 3 , 7 ) be C . Let ∣ A D ∣ = a , ∣ B E ∣ = b , ∣ F C ∣ = c , such that ∣ F A ∣ = L − a , ∣ D B ∣ = L − b , ∣ E C ∣ = L − c . Since △ D E F is equilateral, therefore
a 2 + ( L − b ) 2 − a ( L − b ) = ∣ A B ∣ 2 = ( 5 − 1 ) 2 + ( 4 − 1 ) 2 = 2 5
b 2 + ( L − c ) 2 − b ( L − c ) = ∣ B C ∣ 2 = ( 3 − 5 ) 2 + ( 7 − 4 ) 2 = 1 3
c 2 + ( L − a ) 2 − c ( L − a ) = ∣ A C ∣ 2 = ( 3 − 1 ) 2 + ( 7 − 1 ) 2 = 4 0 .
Solving for L , we get
L = a + 2 c + 1 6 0 − 3 c 2 = b + 2 a + 1 0 0 − 3 a 2 = c + 2 b + 5 2 − 3 b 2
⟹ 3 L = 2 3 ( a + b + c ) + 2 1 ( 1 0 0 − 3 a 2 + 5 2 − 3 b 2 + 1 6 0 − 3 c 2 ) ⟹ 6 L = 3 ( a + b + c ) + 1 0 0 − 3 a 2 + 5 2 − 3 b 2 + 1 6 0 − 3 c 2 .
Now, ( 3 a + 1 0 0 − 3 a 2 ) 2 ≤ 4 ( a 2 + a 2 + a 2 + 1 0 0 − 3 a 2 ) = 4 0 0 ⟹ 3 a + 1 0 0 − 3 a 2 ≤ 2 0 (Cauchy-Schwarz inequality)
Similarly, 3 b + 5 2 − 3 b 2 ≤ 4 1 3
and 3 c + 1 6 0 − 3 c 2 ≤ 8 1 0 .
Hence, 6 L ≤ 2 0 + 4 1 3 + 8 1 0 ⟹ L ≤ 6 1 ( 2 0 + 4 1 3 + 8 1 0 ) ≈ 9 . 9 5 3 4 .
So, the maximum value of L is 9 . 9 5 3 4 .
I found the maximum to be 9.673.
Log in to reply
9.673118389725882
Your solution is not complete. You do not show that this value of 9.9534 can actually be attained.
The largest such equilateral triangle is the antipedal triangle of the Fermat point. The area of this triangle is given by Δ ′ = 2 Δ ( 3 3 cot ω + 1 ) , where Δ is the area of triangle A B C , and ω is its Brocard angle.
Plugging everything in, we get Δ ′ = 1 8 + 1 3 3 . Then the side length of the equilateral triangle is 5 2 + 2 4 3 ≈ 9 . 6 7 3 .
References:
https://www.cut-the-knot.org/Generalization/fermat_point.shtml
https://mathworld.wolfram.com/FermatPoints.html