Fitting an equilateral triangle to three points
Three points in the Cartesian plane are given by: A ( 1 , 1 ) , B ( 5 , 4 ) , C ( 3 , 7 ) . You want to draw an equilateral triangle of side length 8 that will pass through A , B and C , with one point on each side. Find that triangle and report as your answer the sum θ + x C + y C , where the angle θ (in degrees), 0 ∘ ≤ θ < 1 2 0 ∘ , is the counter-clockwise angle of rotation of the triangle with respect to the standard orientation of an equilateral triangle which has one side parallel to the x-axis and the opposing vertex directly above it. And ( x C , y C ) are the coordinates of the center of the triangle.
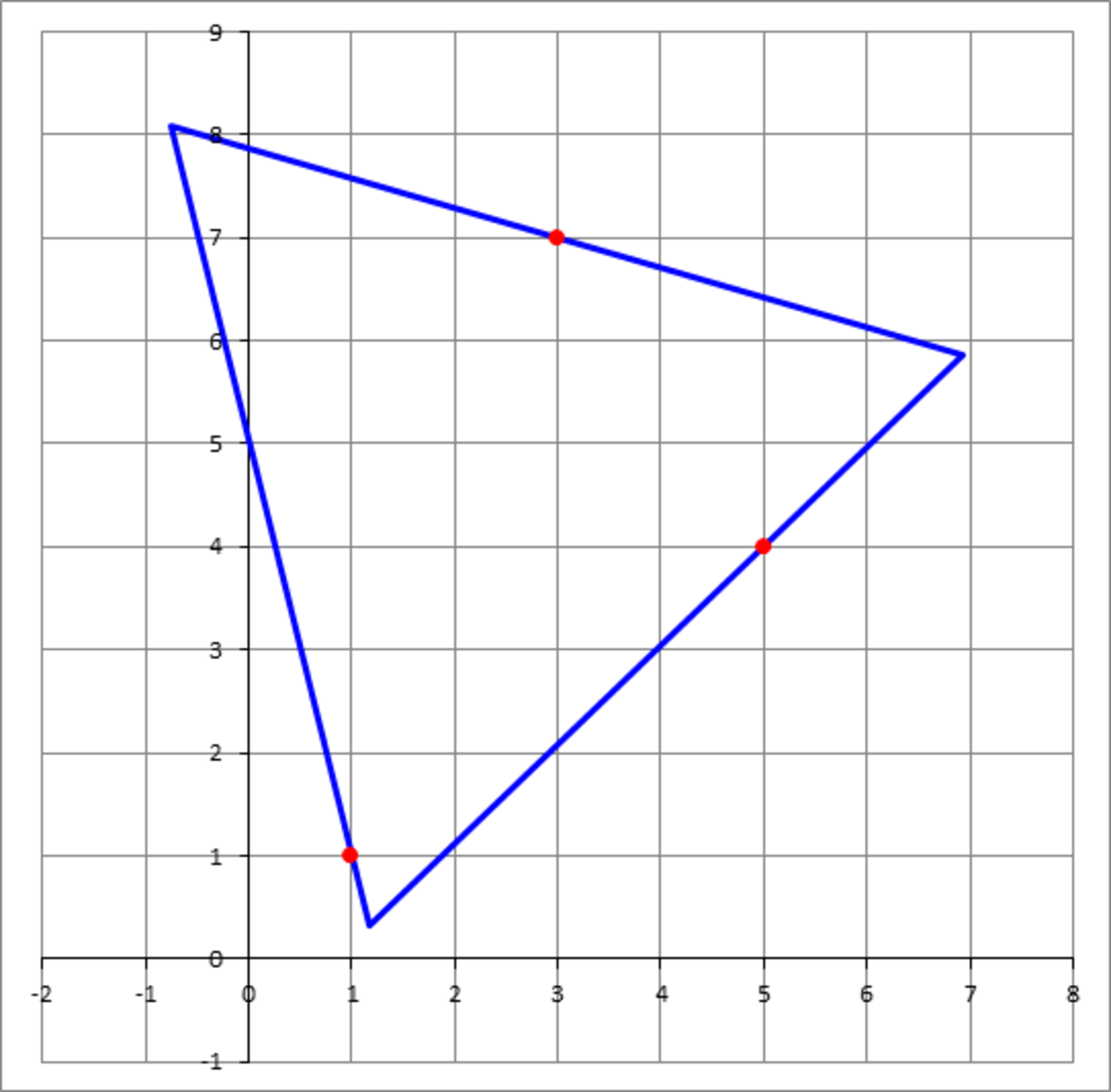
The answer is 51.07.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Try θ = 4 5 ° Then you get an exact equilateral triangle of sides 3 8 + 1 6 3
Log in to reply
Can I have the x c , y c coordinates for that triangle?
Draw A B , B C , and A C , and let D be the vertex of the equilateral triangle nearest to A , E be the vertex of the equilateral triangle nearest to B , and F be the vertex of the equilateral triangle nearest to C . Also let a = A D , b = B E , and c = C F , so that 8 − a = A F , 8 − b = B D , and 8 − c = C E .
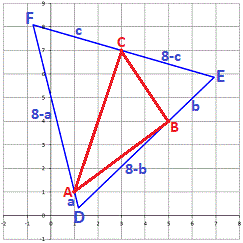
By the distance formula, A B 2 = ( 5 − 1 ) 2 + ( 4 − 1 ) 2 = 2 5 , B C 2 = ( 3 − 5 ) 2 + ( 7 − 4 ) 2 = 1 3 , and A C 2 = ( 3 − 1 ) 2 + ( 7 − 1 ) 2 = 4 0 .
Since △ D E F is an equilateral triangle, ∠ A D B = 6 0 ° , so by the law of cosines on △ A B D , A B 2 = A D 2 + B D 2 − 2 ⋅ A D ⋅ B D ⋅ cos 6 0 ° or 2 5 = a 2 + ( 8 − b ) 2 − a ( 8 − b ) . Similarly on △ B C E and △ A C F , 1 3 = b 2 + ( 8 − c ) 2 − b ( 8 − c ) and 4 0 = c 2 + ( 8 − a ) 2 − c ( 8 − a ) , and these three equations solve to a ≈ 0 . 7 0 2 9 , b ≈ 2 . 6 8 5 7 , c ≈ 3 . 9 0 2 1 for a < b < c .
From A D ≈ 0 . 7 0 2 9 0 we have ( x D − 1 ) 2 + ( y D − 1 ) 2 = 0 . 7 0 2 9 2 and from B D ≈ 8 − 2 . 6 8 5 7 ≈ 5 . 3 1 4 3 we have ( x D − 5 ) 2 + ( y D − 4 ) 2 = 5 . 3 1 4 3 2 , which solves to x D ≈ 1 . 1 6 8 4 and y D ≈ 0 . 3 1 7 6 ) for y D < 1 . Similarly, from B E ≈ 2 . 6 8 5 7 we have ( x E − 5 ) 2 + ( y E − 4 ) 2 = 2 . 6 8 5 7 2 and from C E ≈ 8 − 3 . 9 0 2 1 ≈ 4 . 0 9 7 9 we have ( x E − 3 ) 2 + ( y E − 7 ) 2 = 4 . 0 9 7 9 2 , which solves to x E ≈ 6 . 9 3 6 4 and y E ≈ 5 . 8 6 1 0 ) for x E > 4 .
Because △ D E F has a side of 8 , its center ( x C , y C ) is 3 8 3 away from both D and E , so ( x C − 1 . 1 6 8 4 ) 2 + ( y C − 0 . 3 1 7 5 ) 2 = ( 3 8 3 ) 2 and ( x C − 6 . 9 3 6 4 ) 2 + ( y C − 5 . 8 6 1 0 ) 2 = ( 3 8 3 ) 2 , which solves to x C ≈ 2 . 4 5 2 2 and y C ≈ 4 . 7 5 4 4 for x < 3 .
Finally, since the slope m of D E is m = x E − x D y E − y D ≈ 6 . 9 3 6 4 − 1 . 1 6 8 4 5 . 8 6 1 0 − 0 . 3 1 7 6 ≈ 0 . 9 6 1 1 , the counter-clockwise angle θ is θ ≈ tan − 1 m ≈ tan − 1 0 . 9 6 1 1 ≈ 4 3 . 8 6 2 5 ° .
Therefore, θ + x C + y C ≈ 4 3 . 8 6 2 5 + 2 . 4 5 2 2 + 4 . 7 5 4 4 ≈ 5 1 . 0 7 .
The equations for ( P 1 , P 2 , P 3 ) are as follows:
P 1 x = x c + R cos ( 9 0 ∘ + θ ) P 1 y = y c + R sin ( 9 0 ∘ + θ ) P 2 x = x c + R cos ( − 3 0 ∘ + θ ) P 2 y = y c + R sin ( − 3 0 ∘ + θ ) P 3 x = x c + R cos ( 2 1 0 ∘ + θ ) P 3 y = y c + R sin ( 2 1 0 ∘ + θ ) R = 3 8
This link has a nice formula for the distance from a point to a line segment, which I used. Find ( x c , y c , θ ) such that the following equations are satisfied. Since we want the distance to be zero, the denominators of the distance equation can be disregarded.
Segment with ( P 1 , P 2 , C )
( P 2 x − P 1 x ) ( P 1 y − C y ) − ( P 1 x − C x ) ( P 2 y − P 1 y ) = 0
Segment with ( P 2 , P 3 , B )
( P 3 x − P 2 x ) ( P 2 y − B y ) − ( P 2 x − B x ) ( P 3 y − P 2 y ) = 0
Segment with ( P 3 , P 1 , A )
( P 1 x − P 3 x ) ( P 3 y − A y ) − ( P 3 x − A x ) ( P 1 y − P 3 y ) = 0
A search algorithm finds the following values for the parameters:
x c ≈ 2 . 4 5 2 y c ≈ 4 . 7 5 4 θ ≈ 4 3 . 8 6 3 ∘