Five Balls Bounce
Harry stacks 5 balls one on top of another, raises them so that the bottom ball is 1 m off the ground, and drops them as shown in the diagram. He has the freedom to set the masses of the five balls to whatever values he pleases.
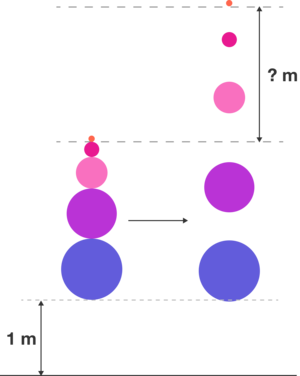
What is the least upper bound of the height to which the top ball can rise above its starting position (in m )?
Assumptions:
- All collisions are perfectly elastic and there is no air resistance.
- You may want to try this related problem as a warmup.
- The figure is not drawn to scale.
The answer is 960.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
What are some of the real life applications of this technology? I am sure there will be issues in launching objects into space with this. But this is amazing and must have some applications.
Log in to reply
In real life it's very difficult to find five balls with masses m 1 < < m 2 < < m 3 < < m 4 . If an upper ball slightly breaks the simmetry of the system it will be launched at a basically unpredictable angle. Someone uploaded an example on youtube (look for "hamster bounces off exercise ball"). Your enthusiasm makes me happy, I'm sorry about not knowing applications of this fact.
Suppose that the balls have masses m 1 < m 2 < m 3 < m 4 < m 5 from the top down. We can solve this problem by considering a sequence of collisions, imagining that m 5 collides with the floor first, then m 5 collides with m 4 , then m 4 collides with m 3 , then m 3 collides with m 2 , and finally m 2 collides with m 1 , where all five balls are initially travelling downwards with speed v = 2 g . Let v 5 = v be the upward speed of m 5 after its collision with the floor, let v 4 be the upward speed of m 4 after its collision with m 5 , let v 3 be the upward speed of m 3 after its collision with m 4 , let v 2 be the upward speed of m 2 after its collision with m 3 , and let v 1 be the upward speed of m 1 after its collision with m 2 . Of course, the final speeds of m 2 , m 3 , m 4 , m 5 after all the collisions will not be the same as v 2 , v 3 , v 4 , v 5 , but v 1 will be the final speed of m 1 , and that is what we want to know.
If a particle of mass m is moving downwards with speed v , and collides with a particle of mass M > m that is moving upwards with speed V then using conservation of momentum and Newton's Law of Restitution (with e = 1 to conserve energy) we deduce that the particle m has upward speed W after the collision, where W = M + m 2 M V + ( M − m ) v and since ( 2 V + v ) − W = M + m 2 m v we deduce that W < 2 V + v .
Thus we deduce that v 4 < 2 v 5 + v = 3 v , v 3 < 2 v 4 + v = 7 v , v 2 < 2 v 3 + v = 1 5 v , while v 1 < 2 v 2 + v = 3 1 v . Thus, if the particle m 1 rises to a height of h metres above its starting position, then h < 3 1 2 − 1 = 9 6 0 . However, it is important to note that all these inequalities are strict , and so it is not possible for h to be equal to 9 6 0 .
We can achieve any height less than 9 6 0 m, however. Considering the m , M ball collision above, we obtain W = 2 V + v in the limit as M m → 0 . The "outcome" v 5 = v , v 4 = 3 v , v 3 = 7 v , v 2 = 1 5 v , v 1 = 3 1 v is an approximation of the case m 1 ≪ m 2 ≪ m 3 ≪ m 4 ≪ m 5 where we consider that each ball is very much more massive than the one above it. As an approximation , then, we say that each lower ball's speed is unaffected by its collision with the ball above it. However, in the real world, it is not possible to choose m 5 infinitely greater than m 4 , m 4 infinitely greater than m 3 , m 3 infinitely greater than m 2 , and m 2 infinitely greater than m 1 , which is what would be required to achieve 9 6 0 metres.
Guess i've forgotten most of the mechanics i was taught in high-school... From your "speed after collision" formula, if M = 10m and V=v, then W = 2.636v ? Not even 3 times as much "bounce", after colliding with a 10x ball? :-s
Log in to reply
To get a 3 v bounceback, the larger ball would have to have infinite mass.
I got confused with the question in the problem: "What is the least upper bound of the height to which...?" But the answer tells us the greatest upper bound.
Log in to reply
No. We want the least upper bound - the smallest number that is an upper bound for possible heights. 970 is an upper bound, as is 960.234. It just happens that 960 is the least upper bound. You can obtain any height less than 960, and cannot exceed 960.
All the balls start hitting each other after having gained the same velocity v = 2 g h , where h = 1 m is the distance of the bottom ball from the ground. The best configuration of masses is one where m 1 > > m 2 > > ⋯ > > m 5 since it allows the highest fraction of kinetic energy to be associated with the fifth ball (a massive object hitting another with smaller mass will make it bounce off with the highest possible velocity). One hit can be thought as a superposition of the following two (bouncing off a wall and the bouncing off a massive object of a body at rest), as showed in the following picture: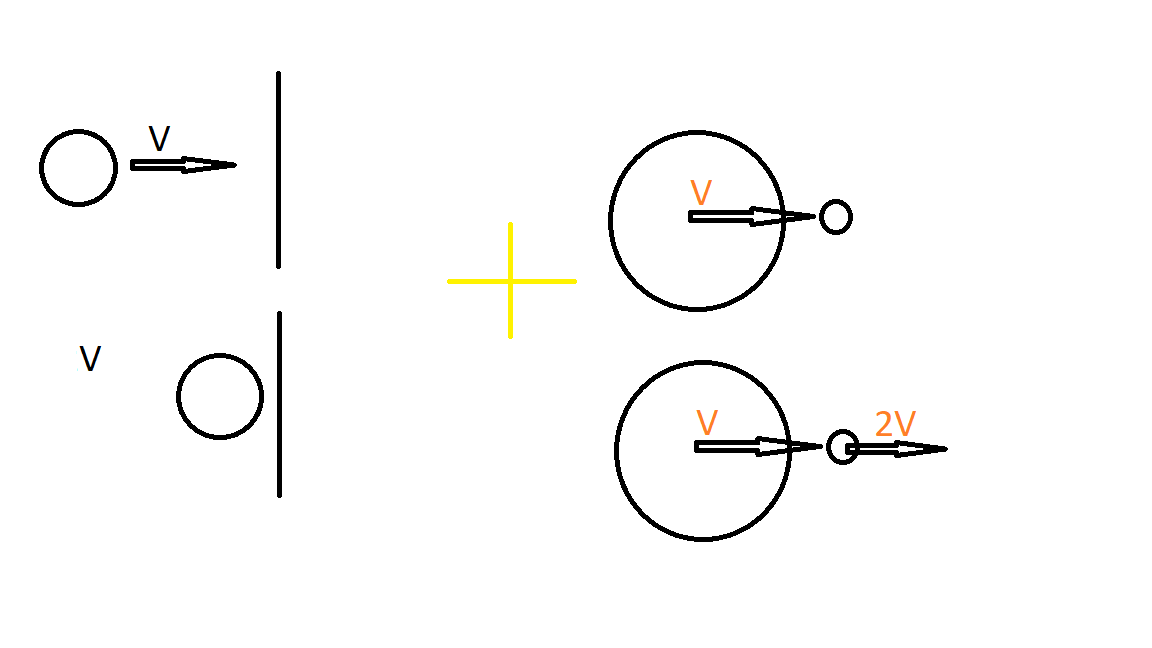 The velocity of the second ball will be
2
⋅
v
+
v
=
3
v
, that of the third one
2
⋅
(
3
v
)
+
1
=
7
v
,...,the fifth one
3
1
v
.
Conservation of energy gives
2
1
⋅
3
1
2
⋅
(
2
g
h
)
2
=
g
H
, hence
d
=
H
−
h
=
9
6
1
m
−
1
h
2
−
h
=
9
6
0
m
.
The velocity of the second ball will be
2
⋅
v
+
v
=
3
v
, that of the third one
2
⋅
(
3
v
)
+
1
=
7
v
,...,the fifth one
3
1
v
.
Conservation of energy gives
2
1
⋅
3
1
2
⋅
(
2
g
h
)
2
=
g
H
, hence
d
=
H
−
h
=
9
6
1
m
−
1
h
2
−
h
=
9
6
0
m
.
Note:considering v = 1 in general v n + 1 = 2 v n + 1 , equivalent to v n + 1 − 2 v n = 1 , satisfied by v n = 2 n − 1 . This consideration can be used to produce a formal proof in conjunction with mathematical induction.