Five congruent circles inscribed in a regular pentagon
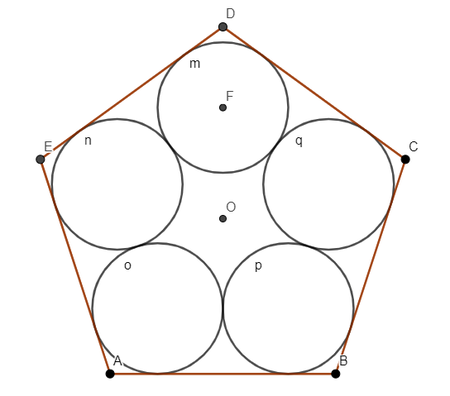
Five congruent circles ( m , n , o , p , q ) are inscribed in a regular pentagon A B C D E of side length 6 , as shown in the figure above. Find the radius r of each of the circles, and submit ⌊ 1 0 4 r ⌋
The answer is 17375.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
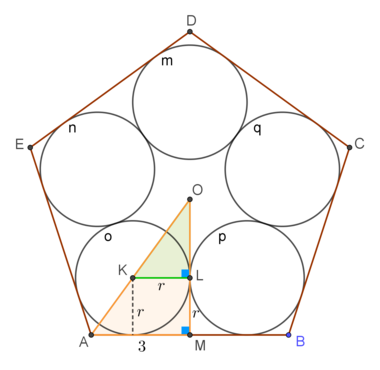 Label the diagram as seen in the figure, where
M
is the midpoint of
A
B
,
K
is the center of
o
and
L
is the common point of circles
o
and
p
. Then,
A
M
=
3
,
K
L
=
L
M
=
r
.
Label the diagram as seen in the figure, where
M
is the midpoint of
A
B
,
K
is the center of
o
and
L
is the common point of circles
o
and
p
. Then,
A
M
=
3
,
K
L
=
L
M
=
r
.
O M is the apothem of the regular pentagon, thus
O M = 2 5 − 2 0 A B = 2 5 − 2 0 6 = 5 − 2 0 3 Triangles △ O K L and △ O A M are similar, hence
A M K L = O M O L ⇒ 3 r = O M O M − r ⇒ r = 3 + O M 3 O M Substituting the value of O M , we get r = 5 − 2 0 + 1 3 ≈ 1 . 7 3 7 5 8 For the answer, ⌊ 1 0 4 r ⌋ = 1 7 3 7 5 .
Label the bottom part of the diagram as follows:
As half the interior angle of a regular pentagon, ∠ C A E = 5 4 ° , and since C E = r , A E = r cot 5 4 ° = 5 − 2 5 r .
Since A E + E F + F B = A B , 5 − 2 5 r + 2 r + 5 − 2 5 r = 6 , which solves to r = 1 + 5 − 2 5 3 ≈ 1 . 7 3 7 5 8 .
Therefore, ⌊ 1 0 4 r ⌋ = 1 7 3 7 5 .