Five Cubes in Dodecahedron

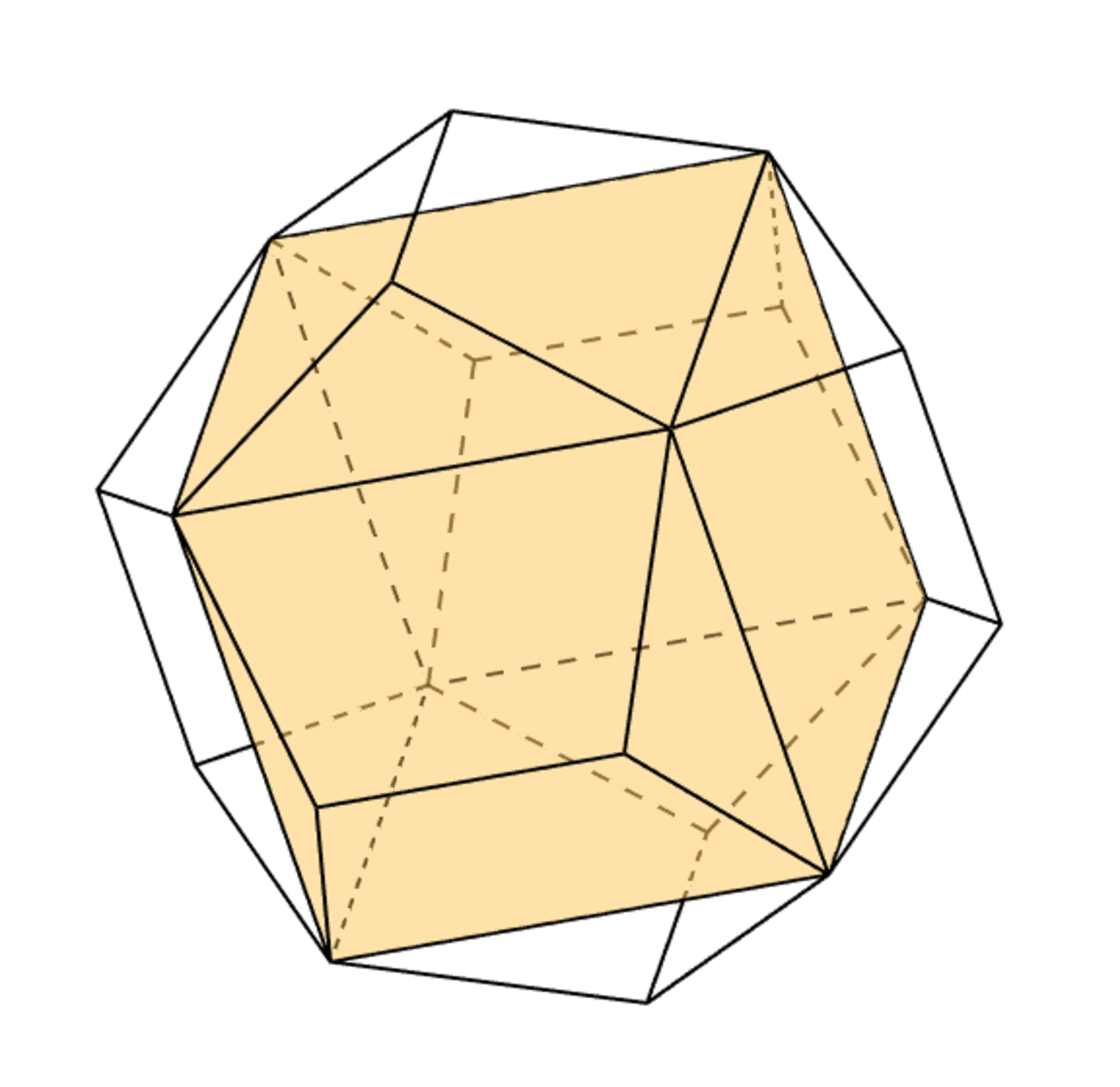
There are five different Cubes with vertices at the vertices of the Dodecahedron. Find ratio $\frac {V_{D}} {V_{RD}}$ , where $V_{RD}$ is volume of common part of five Cubes with vertices in Dodecahedron vertices, and $V_{D}$ - the Dodecahedron volume. If ratio $\frac {V_{D}} {V_{RD}}$ is equal to $\frac {3A+B \sqrt{A}} {2A}$ , where $A$ and $B$ are positive coprime integers, B - square free, give $A+B$ as answer.

Picture is one cube in Dodecahedron.