Five in Three
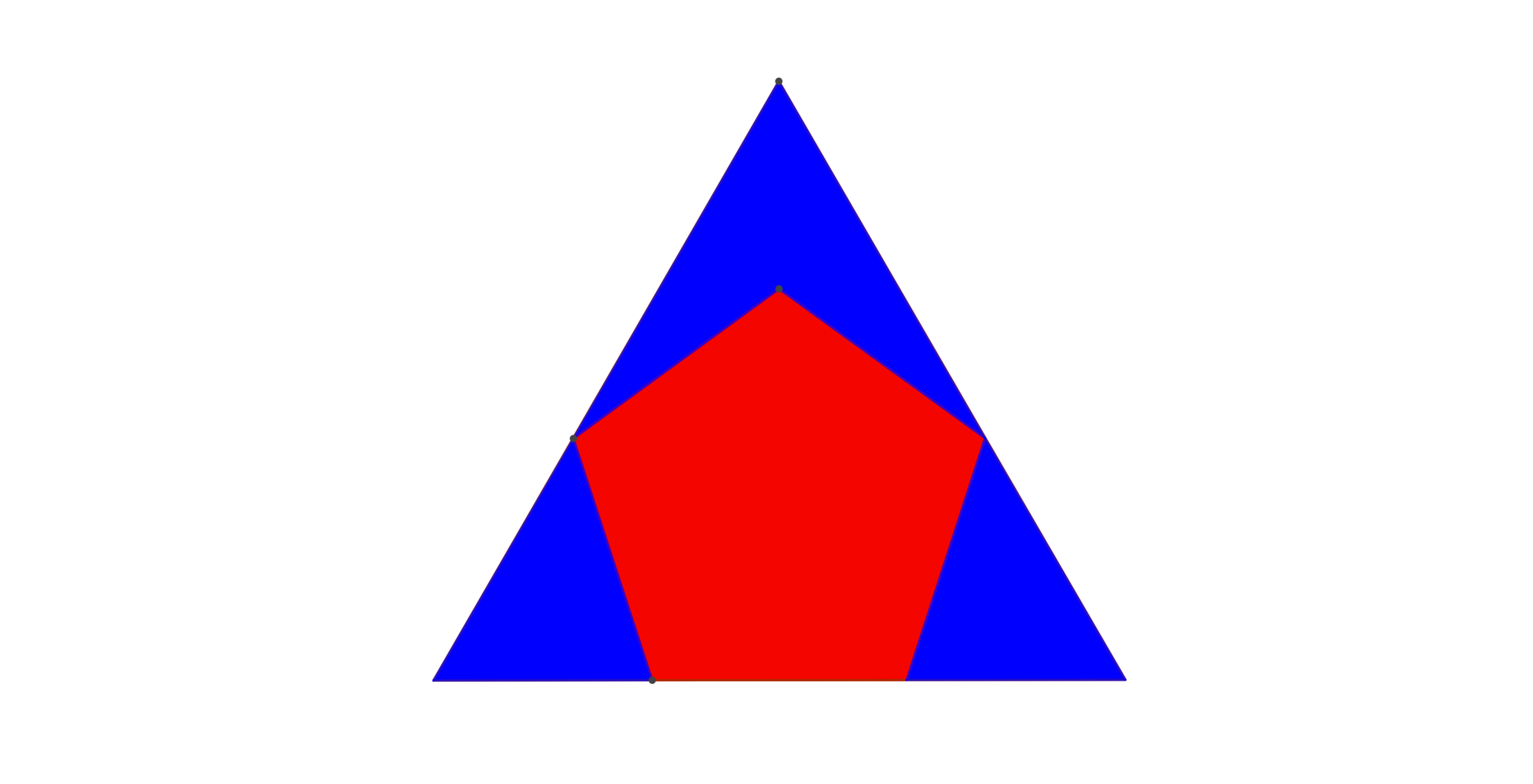
This figure depicts a regular pentagon inscribed in an equilateral triangle. Which color represents the greater area? Inspiration: here
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's assume the pentagon has side length 1.
Solve blue △ B G C . Its angles are easily deduced. ∠ G = 6 0 ∘ and ∠ C = 4 8 ∘
By the law of sines, B G = sin 6 0 ∘ sin 4 8 ∘ ≈ . 8 5 8
Since △ F A E and △ B G C are congruent, F A = B G and F G = 2 × B G + 1 ≈ 2 . 7 1 6
So △ F G H = 4 3 × F G 2 ≈ 3 . 1 9 5
The red area of the pentagon is 4 5 × 1 + 5 2 × A B 2 ≈ 1 . 7 2
Thus the total blue area is 3 . 1 9 5 − 1 . 7 2 ≈ 1 . 4 7 5 < 1 . 7 2
Red wins.