Five Similar Rectangles
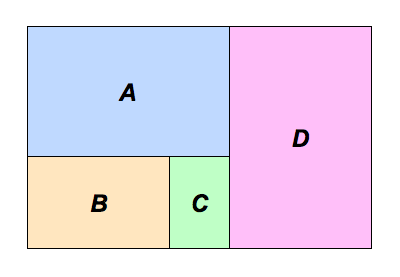
The four rectangles A , B , C , and D below, as well as the big rectangle they compose, are all similar to each other. The ratio of the area of A to the area of B can be written as a : b , where a and b are positive coprime integers. Give a + b .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Only one correction: the equation is k^4 - 2k^2 - 1 = 0.
Let l ( X ) and w ( X ) denote the length and width of rectangle X , where X = A , B , C or D . WLOG, let l ( C ) = 1 and w ( C ) = x . So w ( X ) / l ( X ) = x . It follows that w ( B ) = 1 , l ( B ) = w ( B ) / x = 1 / x , l ( A ) = l ( B ) + w ( C ) = 1 / x + x , w ( A ) = x ⋅ l ( A ) = 1 + x 2 , l ( D ) = w ( A ) + l ( C ) = 2 + x 2 , and w ( D ) = x ⋅ l ( D ) = 2 x + x 3 . Then w ( A ∪ B ∪ C ∪ D ) = x ⋅ l ( A ∪ B ∪ C ∪ D ) , l ( D ) = x ⋅ [ l ( A ) + w ( D ) ] , 2 + x 2 = x ( 1 / x + x + 2 x + x 3 ) , x 4 + 2 x 2 = 1 , ( 1 + x 2 ) 2 = 2 . Hence a / b = [ w ( A ) / w ( B ) ] 2 = ( 1 + x 2 ) 2 = 2 ; and so a + b = 2 + 1 = 3 .
Let short side be denoted by the capital letter, with E the containing rectangle. k times this is the longer side.
From the lengths in the fig, we get the following.
kE=kA+D...........1
kA=kB+C...........2
kC=B..................So C=B/k...................3
kD=A+B.............So D=(A+B)/k............4
E=A+B...............5
Substituting C, D, E from 3, 4, 5 into 1 and 2, we get:-
Into 1 :- k(A+B)=kA+(A+B)/k...........So kB-B/k=A/k.......
⟹
B
A
=
k
2
−
1
..............................6
Into 2 :- kA=kB + B/k....................................................
⟹
B
A
=
1
+
k
2
1
.............7
∴
k
2
−
1
=
1
+
k
2
1
,
⟹
k
4
−
2
k
2
−
1
=
0
.
S
o
l
v
i
n
g
t
h
e
q
u
a
d
r
a
t
i
c
i
n
x
2
,
w
e
g
e
t
x
2
=
1
+
2
,
s
i
n
c
e
x
2
c
a
n
o
n
l
y
b
e
p
o
s
i
t
i
v
e
.
A
r
e
a
o
f
B
A
r
e
a
o
f
A
=
k
B
2
k
A
2
=
(
k
2
−
1
)
2
=
(
1
+
2
−
1
)
2
=
2
=
1
2
=
b
a
.
S
o
a
+
b
=
2
+
1
=
3
.
Let the short side s c of C be 1 and its long side l c = k . Then, we have:
\(\begin{array} {} \Rightarrow s_b=k & \Rightarrow l_b=k^2 \\ \Rightarrow l_a=k^2+1&\Rightarrow s_a= k +\dfrac{1}{k} \\ \Rightarrow l_d=2k+\dfrac {1} {k} & \Rightarrow s_d=2+\dfrac {1} {k ^2} \\ \Rightarrow s_{Big} =2k+\dfrac {1} {k} & \Rightarrow l_{Big} =k^2+3+\dfrac {1} {k ^2} \end{array} \)
And,
\begin{aligned} \frac{l_{Big}}{s_{Big}} & =k \\ \Rightarrow k^2+3+\frac {1} {k^2} & =2k^2 +1\\ k^4-2k^2 - 1&=0 \\ \Rightarrow k^2 & =1 +\sqrt {2} \end{aligned} \end {equation}
Now,
\begin{aligned} \frac {a} {b} & =\frac {s_al_a} {s_b l_b} \\&= \frac {(k^2 +1)^2} {k^4}\\&= \left(\frac {2+\sqrt{2}}{1 +\sqrt {2}}\right) \\&= \left(\frac {(2+\sqrt {2}) (\sqrt {2} - 1)}{(1+\sqrt {2}) (\sqrt {2}-1)} \right) ^2 \\&=(\sqrt {2}) ^2 =2 \end{aligned} \end {equation}
⇒ a + b = 2 + 1 = 3